题目内容
6.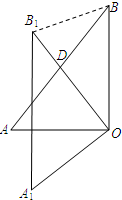 如图,△AOB中,∠AOB=90°,AO=6,BO=8,将△AOB绕顶点O逆时针旋转到△A1OB1处,此时线段OB1与AB的交点D恰好为AB的中点,则线段BB1的长度为$\frac{8\sqrt{10}}{5}$.
如图,△AOB中,∠AOB=90°,AO=6,BO=8,将△AOB绕顶点O逆时针旋转到△A1OB1处,此时线段OB1与AB的交点D恰好为AB的中点,则线段BB1的长度为$\frac{8\sqrt{10}}{5}$.
分析 A1B1与OA相交于点E,作B1H⊥OB于点H,如图,利用勾股定理得到AB=10,再根据直角三角形斜边上的中线性质得OD=AD=DB,则∠1=∠A,接着根据旋转的性质得∠3=∠2,A1B1=AB=10,OB1=OB=8,OA1=OA=6,易得∠2+∠1=90°,所以∠OEB1=90°,于是可利用面积法计算出OE=$\frac{24}{5}$,则可根据勾股定理计算出B1E=$\frac{32}{5}$,再由四边形OEB1H为矩形得到B1H=OE=$\frac{24}{5}$,OH=EB1=$\frac{32}{5}$,得到BH=OB-OH=$\frac{8}{5}$,然后在Rt△B1BH中利用勾股定理可计算出BB1的长.
解答 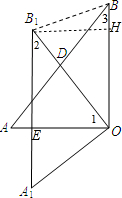 解:A1B1与OA相交于点E,作B1H⊥OB于点H,如图,
解:A1B1与OA相交于点E,作B1H⊥OB于点H,如图,
∵∠AOB=90°,AO=6,BO=8,
∴AB=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∵D为AB的中点,
∴OD=AD=DB,
∴∠1=∠A,
∵△AOB绕顶点O逆时针旋转得到△A1OB1,
∴∠3=∠2,A1B1=AB=10,OB1=OB=8,OA1=OA=6,
∵∠3+∠A=90°,
∴∠2+∠1=90°,
∴∠OEB1=90°,
∵$\frac{1}{2}$OE•A1B1=$\frac{1}{2}$OB1•OA1,
∴OE=$\frac{6×8}{10}$=$\frac{24}{5}$,
在Rt△OEB1中,B1E=$\sqrt{{8}^{2}-(\frac{24}{5})^{2}}$=$\frac{32}{5}$,
易得四边形OEB1H为矩形,
∴B1H=OE=$\frac{24}{5}$,OH=EB1=$\frac{32}{5}$,
∴BH=OB-OH=$\frac{8}{5}$,
在Rt△B1BH中,BB1=$\sqrt{(\frac{24}{5})^{2}+(\frac{8}{5})^{2}}$=$\frac{8\sqrt{10}}{5}$.
故答案为$\frac{8\sqrt{10}}{5}$.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了全等三角形的判定与性质和正方形的性质.

| A. | $y=[{\frac{x+1}{10}}]$ | B. | $y=[{\frac{x+2}{10}}]$ | C. | $y=[{\frac{x+3}{10}}]$ | D. | $y=[{\frac{x+4}{10}}]$ |
| A. | $\frac{-a+b}{a-b}$=-1 | B. | $\frac{{a}^{2}+{b}^{2}}{a+b}$=a+b | C. | $\frac{2a-b}{2a+b}$=$\frac{a-b}{a+b}$ | D. | $\frac{{a}^{2}-{b}^{2}}{a+b}$=a+b |
| A. | -8 | B. | -$\frac{1}{8}$ | C. | 8 | D. | $\frac{1}{2}$ |
| A. |  | B. |  | ||
| C. |  | D. |  |
| A. | $\sqrt{2}$:1 | B. | 1:$\sqrt{3}$ | C. | 1:2 | D. | 1:$\sqrt{2}$ |
 如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,点E是边BC的中点.
如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,点E是边BC的中点.