题目内容
5. 如图,已知四边形ABCD是正方形,△AEF是等边三角形,E、F分别位于DC边和BC边上.
如图,已知四边形ABCD是正方形,△AEF是等边三角形,E、F分别位于DC边和BC边上.(1)求∠DAE的度数;
(2)若正方形ABCD的边长为1,求等边三角形AEF的面积;
(3)将△AEF绕着点E逆时针旋转m(0<m<180)度,使得点A落在正方形ABCD的边上,求m的值.
分析 (1)由四边形ABCD是正方形,得到AB=AD,AF=AE,∠B=∠D=90°,根据全等三角形的性质得到∠DAE=∠BAF,于是得到结论;
(2)设BF=x,由(1)可知DE=BF=x,则,CF=CE=1-x根据勾股定理列方程得到x=2$-\sqrt{3}$,根据图形的面积公式即可得到结论;
(3)依题意,点A可落在AB边上或BC边上.当点A落在AB边上时,设此时点A的对应点为M,则EA=EM,根据等腰三角形的性质得到∠EMB=75°,于是得到m=∠AEM=180°-75°-75°=30°,当点A落在边BC上时,得到m=∠AEF=60°.
解答 解:(1)∵四边形ABCD是正方形,
∴AB=AD,AF=AE,∠B=∠D=90°,
在Rt△ABF与Rt△ADE,$\left\{\begin{array}{l}{AB=AD}\\{AF=AE}\end{array}\right.$,
∴Rt△ABF≌Rt△ADE,
∴∠DAE=∠BAF
又∠DAE+∠BAF=∠BAD-∠EAF=90°-60°=30°
∴∠DAE=15°;
(2)设BF=x,由(1)可知DE=BF=x,则,CF=CE=1-x
AB2+BF2=AF2,CF2+CE2=EF2,AF=EF,得:12+x2=2(1-x)2
x1=2+$\sqrt{3}$,x2=2$-\sqrt{3}$,
∵0<x<1,
∴x1=2+$\sqrt{3}$ (舍去),x=2$-\sqrt{3}$,
∴S△AEF=S四边形ABCD-2S△ABF-S△EFC=12-2×$\frac{1}{2}×$1×(2-$\sqrt{3}$)-$\frac{1}{2}×$($\sqrt{3}$-1)2=2$\sqrt{3}$-3;
(3)依题意,点A可落在AB边上或BC边上.
当点A落在AB边上时,设此时点A的对应点为M,则EA=EM,
∵∠EAB=75°,
∴∠EMB=75°,
∴m=∠AEM=180°-75°-75°=30°,
当点A落在边BC上时,
∵EA=EF,点A旋转后与点F重合,
∴m=∠AEF=60°,
综上,m=30°或m=60°.
点评 本题考查了旋转的性质,等边三角形的性质,正方形的性质,全等三角形的判定和性质,熟练掌握各性质定理是解题的关键.

 53随堂测系列答案
53随堂测系列答案| 星 期 | 一 | 二 | 三 | 四 | 五 |
| 收盘价的变化(与前一 天收盘价比较) | +7 | +5 | -3 | -6 | +8 |
(2)本周黄金收盘时的最高价是262元,最低价分别是253元;
(3)上周,小王以周五的收盘价250元/克买入黄金1000克,已知买入与卖出时均需支付成交金额的千分之五的交易费,卖出黄金时需支付成交金额的千分之三的印花税.本周,小王以周五的收盘价全部卖出黄金1000克,他的收益情况如何?
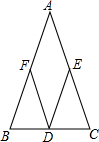 已知:如图,等腰△ABC中,AB=AC,D是BC的中点,DE∥AB,DF∥AC,求证:四边形AFDE是菱形.
已知:如图,等腰△ABC中,AB=AC,D是BC的中点,DE∥AB,DF∥AC,求证:四边形AFDE是菱形.
 在平面直角坐标系中,小方格都是边长为1的正方形,△ABC≌△DEF,其中点A、B、C、D都在格点上,点E、F在方格线上,请你解答下列问题:
在平面直角坐标系中,小方格都是边长为1的正方形,△ABC≌△DEF,其中点A、B、C、D都在格点上,点E、F在方格线上,请你解答下列问题: 如图,在Rt△ABC中,AB=AC=4$\sqrt{2}$.一动点P从点B出发,沿BC方向以每秒1个单位长度的速度匀速运动,到达点C即停止.在整个运动过程中,过点P作PD⊥BC与Rt△ABC的直角边相交于点D,以PD为直角边在PD左侧作等腰直角三角形PDE.在整个运动过程中,设△ABC与△PDE重叠部分的面积为S,设运动时间为t秒.
如图,在Rt△ABC中,AB=AC=4$\sqrt{2}$.一动点P从点B出发,沿BC方向以每秒1个单位长度的速度匀速运动,到达点C即停止.在整个运动过程中,过点P作PD⊥BC与Rt△ABC的直角边相交于点D,以PD为直角边在PD左侧作等腰直角三角形PDE.在整个运动过程中,设△ABC与△PDE重叠部分的面积为S,设运动时间为t秒. 在如图所示的方格纸中,每个小正方形方格的边长都为1,△ABC的三个顶点在格点上.
在如图所示的方格纸中,每个小正方形方格的边长都为1,△ABC的三个顶点在格点上.