Question

19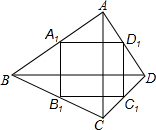．如图，四边形ABCD的两条对角线AC，BD互相垂直，A₁，B₁，C₁，D₁是四边形ABCD对应边上的中点．如果AC=8，BD=10，那么四边形A₁B₁C₁D₁周长为18．

Answer 1

分析 根据三角形的中位线的性质可得A₁B₁=$\frac{1}{2}$AC，D₁C₁=$\frac{1}{2}$AC，A₁D₁=$\frac{1}{2}$BD，B₁C₁=$\frac{1}{2}$BD，根据条件AC=8，BD=10可得A₁B₁=C1D1=4，A₁D₁=B₁C₁=5，进而可得答案．

解答 解：∵A₁，B₁，C₁，D₁是四边形ABCD对应边上的中点，
∴A₁B₁=$\frac{1}{2}$AC，D₁C₁=$\frac{1}{2}$AC，A₁D₁=$\frac{1}{2}$BD，B₁C₁=$\frac{1}{2}$BD，
∵AC=8，BD=10，
∴A₁B₁=C1D1=4，A₁D₁=B₁C₁=5，
∴四边形A₁B₁C₁D₁周长为4+4+5+5=18，
故答案为：18．

点评 此题主要考查了中点四边形，关键是掌握三角形的中位线平行于第三边，且等于第三边的一半．