题目内容
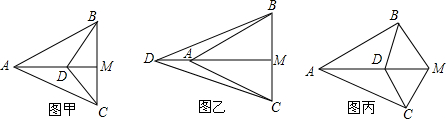
7. 在下列四个条件中:①AB=DC;②∠BAE=∠CDE;③BD=AC;④∠B=∠C.请
在下列四个条件中:①AB=DC;②∠BAE=∠CDE;③BD=AC;④∠B=∠C.请选出两个作为条件,得出△AED是等腰三角形(写出一个即可),并加以证明.
已知:AB=DC,∠B=∠C;
求证:△AED是等腰三角形.
证明:
分析 根据“有两条边相等的三角形是等腰三角形”、“等角对等边”判定等腰三角形即可.
解答 解: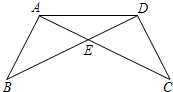 可以选择填写:①AB=DC;④∠B=∠C;或①AB=DC;②∠BAE=∠CDE.
可以选择填写:①AB=DC;④∠B=∠C;或①AB=DC;②∠BAE=∠CDE.
或①AB=DC;③BD=AC;.
证明:下面以①④为例证明
在△AEB和△DEC中,
$\left\{\begin{array}{l}{∠BEA=∠CDE}\\{∠B=∠C}\\{AB=DC}\end{array}\right.$
∴△AEB≌△DEC
∴AE=DE
∴△AED是等腰三角形.
点评 本题考查了三角形全等的判定与性质,等腰三角形的判定与性质,熟记三角形的全等判定定理是解决此题的关键与基础.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.等腰三角形的一个角是50°,则它顶角的度数是( )
| A. | 80°或50° | B. | 80° | C. | 80°或65° | D. | 65° |
18. 如图所示,河对岸有水塔CD.今在A处测得塔顶C的仰角为30°,前进20米到达B处,又测得C的仰角为45°,则塔高CD(精确到0.1m)是( )m.
如图所示,河对岸有水塔CD.今在A处测得塔顶C的仰角为30°,前进20米到达B处,又测得C的仰角为45°,则塔高CD(精确到0.1m)是( )m.
 如图所示,河对岸有水塔CD.今在A处测得塔顶C的仰角为30°,前进20米到达B处,又测得C的仰角为45°,则塔高CD(精确到0.1m)是( )m.
如图所示,河对岸有水塔CD.今在A处测得塔顶C的仰角为30°,前进20米到达B处,又测得C的仰角为45°,则塔高CD(精确到0.1m)是( )m.| A. | 25.3 | B. | 26.3 | C. | 27.3 | D. | 28.3 |
15. 如图是我市某一天内的气温变化图,根据图形,下列说法中错误的是( )
如图是我市某一天内的气温变化图,根据图形,下列说法中错误的是( )
 如图是我市某一天内的气温变化图,根据图形,下列说法中错误的是( )
如图是我市某一天内的气温变化图,根据图形,下列说法中错误的是( )| A. | 这一天中最高气温是24℃ | |
| B. | 这一天中最高气温与最低气温的差为14℃ | |
| C. | 这一天中2时至14时之间的气温在逐渐升高 | |
| D. | 这一天中只有14时至24时之间的气温在逐渐降低 |
12.将下列长度的三根木棍首尾顺次连接,能组成三角形的是( )
| A. | 4,5,10 | B. | 3,4,5 | C. | 1,3,4 | D. | 1,2,3 |
 如图所示,DE∥BC,∠1=∠2,求证:EF∥AB.
如图所示,DE∥BC,∠1=∠2,求证:EF∥AB.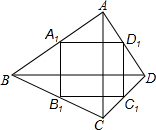 如图,四边形ABCD的两条对角线AC,BD互相垂直,A1,B1,C1,D1是四边形ABCD对应边上的中点.如果AC=8,BD=10,那么四边形A1B1C1D1周长为18.
如图,四边形ABCD的两条对角线AC,BD互相垂直,A1,B1,C1,D1是四边形ABCD对应边上的中点.如果AC=8,BD=10,那么四边形A1B1C1D1周长为18.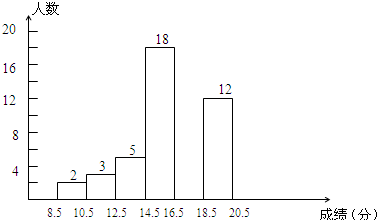 某初中九年级共有700名学生,进行体育测试,包括两项内容:立定跳远和长跑(男子1000米、女子800米),满分各为10分,共20分,得分取整数.随机抽取50名学生的测试成绩进行统计分析,将所有成绩由低到高分成6组,并绘制成如下图所示的频数分布直方图,请结合直方图提供的信息,回答下列问题:
某初中九年级共有700名学生,进行体育测试,包括两项内容:立定跳远和长跑(男子1000米、女子800米),满分各为10分,共20分,得分取整数.随机抽取50名学生的测试成绩进行统计分析,将所有成绩由低到高分成6组,并绘制成如下图所示的频数分布直方图,请结合直方图提供的信息,回答下列问题: