题目内容
10.如图,四边形ABCD是菱形,对角线AC与BD交于点O,且AC=80,BD=60.动点M,N分别以每秒1个单位的速度从点A,D同时出发,分别沿A→O→D和D→A运动,当点N到达点A时,M,N同时停止运动.设运动时间为t秒.(1)求菱形ABCD的周长.
(2)设△DMN的面积为S,求S关于t的解析式,并求S的最大值(提示:需分两种情况讨论).
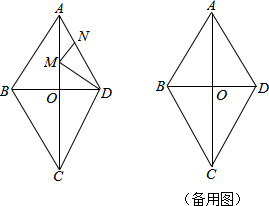
分析 (1)根据勾股定理及菱形的性质,求出菱形的周长;
(2)在动点M、N运动过程中:①当0<t≤40时,如答图1所示,②当40<t≤50时,如答图2所示.分别求出S的关系式,然后利用二次函数的性质求出最大值.
解答 解:(1)在菱形ABCD中,
∵四边形ABCD是菱形,对角线AC与BD交于点O,且AC=80,BD=60,
∴OA=40,OD=30,
∵AC⊥BD,
∴AD=$\sqrt{{{30}^2}+{{40}^2}}$=50.
∴菱形ABCD的周长为200.
(2)过点M作MP⊥AD,垂足为点P.
①当0<t≤40时,如图1,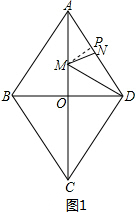
∵$sin∠OAD=\frac{MP}{AM}=\frac{OD}{AD}=\frac{3}{5}$,
∴MP=AM•sin∠OAD=$\frac{3}{5}t$.
∴$s=\frac{1}{2}DN•MP=\frac{3}{10}{t^2}$.
∵S随t的增大而增大,
∴当t=40时,最大值为480;
②当40<t≤50时,如图2,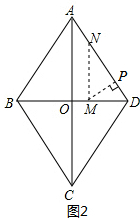
∴MD=80-t.
∵$sin∠ADO=\frac{MP}{MD}=\frac{AO}{AD}$,
∴MP=$\frac{4}{5}({70-t})$.
∴${S}_{△DMN}=\frac{1}{2}DN•MP$=$\frac{1}{2}×t×\frac{4}{5}(70-t)$=$-\frac{2}{5}{t}^{2}+28t$=$-\frac{2}{5}(t-35)^{2}$+490.
∵S随t的增大而减小,
∴当t=40时,最大值为480.
综上所述,S的最大值为480.
点评 本题考查了菱形的性质、勾股定理、解直角三角形、二次函数极值等知识点,涉及考点较多,有一定的难度.第(2)问中,动点M在线段AO和OD上运动时,是两种不同的情形,需要分类讨论;

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案| A. | 1 620度 | B. | 1 440度 | C. | 720度 | D. | 360度 |
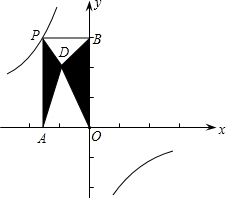 如图,P是反比例函数y=$\frac{k}{x}$的图象上任意点,过点P分别作坐标轴的垂线与坐标轴构成矩形OAPB,点D是对角线OP上的动点,连接DA、DB,若图中阴影部分的面积是5,则反比例函数的关系式是( )
如图,P是反比例函数y=$\frac{k}{x}$的图象上任意点,过点P分别作坐标轴的垂线与坐标轴构成矩形OAPB,点D是对角线OP上的动点,连接DA、DB,若图中阴影部分的面积是5,则反比例函数的关系式是( )| A. | y=-$\frac{5}{x}$ | B. | y=-$\frac{8}{x}$ | C. | y=-$\frac{10}{x}$ | D. | y=-$\frac{12}{x}$ |
 如图所示,河对岸有水塔CD.今在A处测得塔顶C的仰角为30°,前进20米到达B处,又测得C的仰角为45°,则塔高CD(精确到0.1m)是( )m.
如图所示,河对岸有水塔CD.今在A处测得塔顶C的仰角为30°,前进20米到达B处,又测得C的仰角为45°,则塔高CD(精确到0.1m)是( )m.| A. | 25.3 | B. | 26.3 | C. | 27.3 | D. | 28.3 |
 如图是我市某一天内的气温变化图,根据图形,下列说法中错误的是( )
如图是我市某一天内的气温变化图,根据图形,下列说法中错误的是( )| A. | 这一天中最高气温是24℃ | |
| B. | 这一天中最高气温与最低气温的差为14℃ | |
| C. | 这一天中2时至14时之间的气温在逐渐升高 | |
| D. | 这一天中只有14时至24时之间的气温在逐渐降低 |
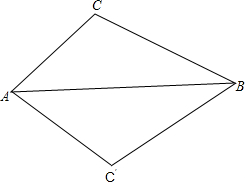 如图所示,把上边的图形沿AB翻折后得到下边的图形,则有三对角对应相等,这三对角分别为∠C=∠C′,∠CAB=∠C′AB,∠CBA=∠C′BA.
如图所示,把上边的图形沿AB翻折后得到下边的图形,则有三对角对应相等,这三对角分别为∠C=∠C′,∠CAB=∠C′AB,∠CBA=∠C′BA. 如图所示,DE∥BC,∠1=∠2,求证:EF∥AB.
如图所示,DE∥BC,∠1=∠2,求证:EF∥AB.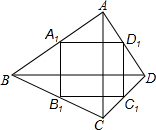 如图,四边形ABCD的两条对角线AC,BD互相垂直,A1,B1,C1,D1是四边形ABCD对应边上的中点.如果AC=8,BD=10,那么四边形A1B1C1D1周长为18.
如图,四边形ABCD的两条对角线AC,BD互相垂直,A1,B1,C1,D1是四边形ABCD对应边上的中点.如果AC=8,BD=10,那么四边形A1B1C1D1周长为18.