题目内容
17.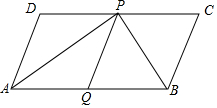 如图,在?ABCD中,AP和BP分别平分∠DAB和∠CBA,PQ∥AD,若AD=5cm,AP=8cm,则△ABP的面积等于24cm2.
如图,在?ABCD中,AP和BP分别平分∠DAB和∠CBA,PQ∥AD,若AD=5cm,AP=8cm,则△ABP的面积等于24cm2.
分析 根据平行四边形性质得出AD∥CB,AB∥CD,推出∠DAB+∠CBA=180°,求出∠PAB+∠PBA=90°,在△APB中求出∠APB=90°,由勾股定理求出BP,证出AD=DP=5,BC=PC=5,得出DC=10=AB,再利用直角三角形面积求法即可得出答案.
解答 解:∵四边形ABCD是平行四边形,
∴AD∥CB,AB∥CD,
∴∠DAB+∠CBA=180°,
又∵AP和BP分别平分∠DAB和∠CBA,
∴∠PAB+∠PBA=$\frac{1}{2}$(∠DAB+∠CBA)=90°,
在△APB中,∠APB=180°-(∠PAB+∠PBA)=90°;
∵AP平分∠DAB,
∴∠DAP=∠PAB,
∵AB∥CD,
∴∠PAB=∠DPA
∴∠DAP=∠DPA
∴△ADP是等腰三角形,
∴AD=DP=5,
同理:PC=CB=5,
即AB=DC=DP+PC=10,
在Rt△APB中,AB=10,AP=8,
∴BP=$\sqrt{1{0}^{2}-{8}^{2}}$=6,
∴△ABP的面积为:$\frac{1}{2}$×6×8=24(cm2).
故答案为:24.
点评 本题考查了平行四边形性质、平行线性质、等腰三角形的性质和判定、三角形的内角和定理、勾股定理等知识点的综合运用,正确得出BP的长是解题关键.

练习册系列答案
相关题目
12.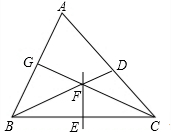 如图,△ABC中,BD是∠ABC的平分线,EF垂直平分BC分别交BC,BD与点E,F,连接CF并延长,交AB于点G,若CG⊥AB,则∠FCB的度数为( )
如图,△ABC中,BD是∠ABC的平分线,EF垂直平分BC分别交BC,BD与点E,F,连接CF并延长,交AB于点G,若CG⊥AB,则∠FCB的度数为( )
 如图,△ABC中,BD是∠ABC的平分线,EF垂直平分BC分别交BC,BD与点E,F,连接CF并延长,交AB于点G,若CG⊥AB,则∠FCB的度数为( )
如图,△ABC中,BD是∠ABC的平分线,EF垂直平分BC分别交BC,BD与点E,F,连接CF并延长,交AB于点G,若CG⊥AB,则∠FCB的度数为( )| A. | 30° | B. | 35° | C. | 40° | D. | 45° |
9. 如图,在Rt△ABC中,∠C=90°,如果AB=5,BC=3,那么AC等于( )
如图,在Rt△ABC中,∠C=90°,如果AB=5,BC=3,那么AC等于( )
 如图,在Rt△ABC中,∠C=90°,如果AB=5,BC=3,那么AC等于( )
如图,在Rt△ABC中,∠C=90°,如果AB=5,BC=3,那么AC等于( )| A. | $\sqrt{34}$ | B. | 3 | C. | 4 | D. | 5 |
7.已知方程3x-2y=5,把它变形为用含x的代数式表示y,正确的是( )
| A. | $y=\frac{3x-5}{2}$ | B. | $y=\frac{3x+5}{2}$ | C. | $y=\frac{-3x+5}{2}$ | D. | $y=\frac{-3x-5}{2}$ |
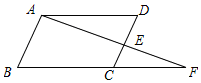 如图,点C、E分别是线段BF、线段CD的中点,AD∥BF.
如图,点C、E分别是线段BF、线段CD的中点,AD∥BF.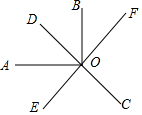 如图,已知直线CD、EF相交于点O,OA⊥OB,且OE平分∠AOC,若∠EOC=60°,则∠BOF=30°.
如图,已知直线CD、EF相交于点O,OA⊥OB,且OE平分∠AOC,若∠EOC=60°,则∠BOF=30°. 如图,△ABC中,AB=AC,BC=3,AD是BC边上的高,且AD=4,则图中阴影部分的面积为3.
如图,△ABC中,AB=AC,BC=3,AD是BC边上的高,且AD=4,则图中阴影部分的面积为3.