题目内容
20.在同一平面内,有4条直线,每两条直线都相交,则交点个数为1或4或7.分析 分情况作出图形,根据图形可得交点个数.
解答 解:如图所示:
故交点个数为1或4或7.
故答案为:1或4或7.
点评 考查了直线、射线、线段,解答此题的关键是找出规律,注意分类思想的应用.

练习册系列答案
相关题目
8.下列各式成立的是( )
| A. | (a+b)2=a2+b2 | B. | (a-b)2=a2-b2 | ||
| C. | -x2+4xy-4xy2=-(x-2y)2 | D. | a2+ab+b2=(a+b)2 |
12.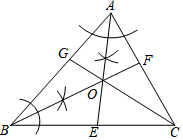 如图,AE与BF交于点O,点O在CG上,根据尺规作图的痕迹,判断下列说法不正确的是( )
如图,AE与BF交于点O,点O在CG上,根据尺规作图的痕迹,判断下列说法不正确的是( )
 如图,AE与BF交于点O,点O在CG上,根据尺规作图的痕迹,判断下列说法不正确的是( )
如图,AE与BF交于点O,点O在CG上,根据尺规作图的痕迹,判断下列说法不正确的是( )| A. | AE、BF是△ABC的内角平分线 | B. | CG也是△ABC的一条内角平分线 | ||
| C. | AO=BO=CO | D. | 点O到△ABC三边的距离相等 |
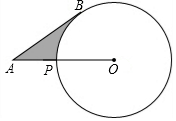 如图,已知A为⊙O外一点,连结OA交⊙O于P,AB为⊙O的切线,B为切点,AP=5cm,AB=5$\sqrt{3}$cm,则劣弧$\widehat{BP}$与AB,AP所围成的阴影的面积是($\frac{25}{2}\sqrt{3}-\frac{25π}{6}$)cm2
如图,已知A为⊙O外一点,连结OA交⊙O于P,AB为⊙O的切线,B为切点,AP=5cm,AB=5$\sqrt{3}$cm,则劣弧$\widehat{BP}$与AB,AP所围成的阴影的面积是($\frac{25}{2}\sqrt{3}-\frac{25π}{6}$)cm2 
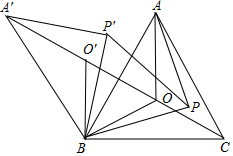 如图,O是锐角三角形ABC内一点,∠AOB=∠BOC=∠COA=120°,P是△ABC内不同于O的另一点;△A′BO′、△A′BP′分别由△AOB、△APB逆时针旋转而得,旋转角都为60°,则下列结论:
如图,O是锐角三角形ABC内一点,∠AOB=∠BOC=∠COA=120°,P是△ABC内不同于O的另一点;△A′BO′、△A′BP′分别由△AOB、△APB逆时针旋转而得,旋转角都为60°,则下列结论: