题目内容
12．
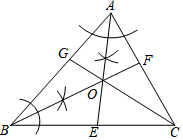如图，AE与BF交于点O，点O在CG上，根据尺规作图的痕迹，判断下列说法不正确的是（ ）| A． | AE、BF是△ABC的内角平分线 | B． | CG也是△ABC的一条内角平分线 | ||
| C． | AO=BO=CO | D． | 点O到△ABC三边的距离相等 |
分析 根据三角形角平分线的性质：三角形三条角平分线交于一点，且到三边的距离相等可以作判断．
解答 解：A、由尺规作图的痕迹可知：AE、BF是△ABC的内角平分线，所以选项A正确；
B、根据三角形三条角平分线交于一点，且点O在CG上，所以CG也是△ABC的一条内角平分线，所以选项B正确；
C、三角形三边中垂线的交点到三个顶点的距离相等，所以选项C不正确；
D、因为角平分线的点到角两边的距离相等得：点O到△ABC三边的距离相等，所以选项D正确；
本题选择说法不正确的，故选C．
点评 本题考查了基本作图-角的平分线、角平分线的性质，明确三角形的角平分线交于同一点，且交点到三边的距离相等．
练习册系列答案
相关题目
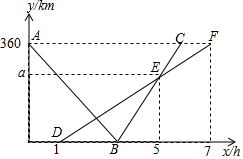快、慢两车分别从相距360km的佳市、哈市两地出发，匀速行驶，先相向而行，慢车在快车出发1h后出发，到达佳市后停止行驶，快车到达哈市后，立即按原路原速返回佳市（快车调头的时间忽略不计），快、慢两车距哈市的路程y1（单位：km），y2（单位：km）与快车出发时间x（单位：h）之间的函数图象如图所示，请结合图象信息解答下列问题：
2．下列计算正确的是（ ）
| A． | $\sqrt{8}$+$\sqrt{2}$=$\sqrt{10}$ | B． | $\sqrt{8}$-$\sqrt{2}$=$\sqrt{2}$ | C． | $\sqrt{8}×\sqrt{2}$=$\sqrt{16}$ | D． | $\sqrt{8}$÷$\sqrt{2}$=$\sqrt{4}$ |