题目内容
11.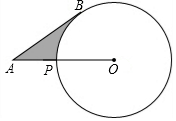 如图,已知A为⊙O外一点,连结OA交⊙O于P,AB为⊙O的切线,B为切点,AP=5cm,AB=5$\sqrt{3}$cm,则劣弧$\widehat{BP}$与AB,AP所围成的阴影的面积是($\frac{25}{2}\sqrt{3}-\frac{25π}{6}$)cm2
如图,已知A为⊙O外一点,连结OA交⊙O于P,AB为⊙O的切线,B为切点,AP=5cm,AB=5$\sqrt{3}$cm,则劣弧$\widehat{BP}$与AB,AP所围成的阴影的面积是($\frac{25}{2}\sqrt{3}-\frac{25π}{6}$)cm2
分析 利用切割线定理可得OP=5cm,OA=10cm,可得出∠BOP=60度;由此可求出扇形OBP的面积.那么劣弧$\widehat{BP}$与AB、AP所围成部分的面积可用△ABO和扇形OBP的面积差求得.
解答 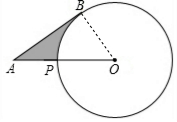 解:连接OB,则∠ABO=90°;
解:连接OB,则∠ABO=90°;
由于AB是⊙O的切线,则有:
AB2=AP•(AP+2OP),即OP=5cm;
在Rt△ABO中,AO=10cm,OB=OP=5cm,因此∠BOP=60°;
∴S阴影=S△AOB-S扇形OBP
=$\frac{1}{2}$×5×5$\sqrt{3}$-$\frac{60π×{5}^{2}}{360}$=$\frac{25}{2}$$\sqrt{3}$-$\frac{25π}{6}$(cm2).
故答案为:($\frac{25}{2}$$\sqrt{3}$-$\frac{25π}{6}$)cm2.
点评 本题主要考查了切线的性质、扇形面积的计算公式等知识,属于基础题,熟练掌握扇形面积的公式是关键.

练习册系列答案
相关题目
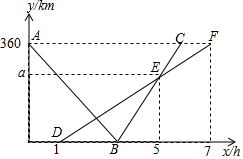 快、慢两车分别从相距360km的佳市、哈市两地出发,匀速行驶,先相向而行,慢车在快车出发1h后出发,到达佳市后停止行驶,快车到达哈市后,立即按原路原速返回佳市(快车调头的时间忽略不计),快、慢两车距哈市的路程y1(单位:km),y2(单位:km)与快车出发时间x(单位:h)之间的函数图象如图所示,请结合图象信息解答下列问题:
快、慢两车分别从相距360km的佳市、哈市两地出发,匀速行驶,先相向而行,慢车在快车出发1h后出发,到达佳市后停止行驶,快车到达哈市后,立即按原路原速返回佳市(快车调头的时间忽略不计),快、慢两车距哈市的路程y1(单位:km),y2(单位:km)与快车出发时间x(单位:h)之间的函数图象如图所示,请结合图象信息解答下列问题: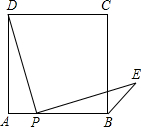 点P是正方形ABCD边AB上一点(不与A、B重合),连接PD并将线段PD绕点P顺时针旋转90°,得线段PE,连接BE,则∠CBE等于45度.
点P是正方形ABCD边AB上一点(不与A、B重合),连接PD并将线段PD绕点P顺时针旋转90°,得线段PE,连接BE,则∠CBE等于45度. 如图,已知三点A、B、C.
如图,已知三点A、B、C.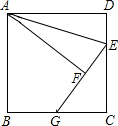 如图,正方形ABCD中,E为CD上一点,以AE为对称轴将△ADE翻折得到△AFE,延长EF交BC于G,若BG=CG,则sin∠EGC=$\frac{4}{5}$.
如图,正方形ABCD中,E为CD上一点,以AE为对称轴将△ADE翻折得到△AFE,延长EF交BC于G,若BG=CG,则sin∠EGC=$\frac{4}{5}$.