题目内容
9.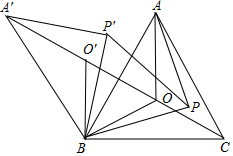 如图,O是锐角三角形ABC内一点,∠AOB=∠BOC=∠COA=120°,P是△ABC内不同于O的另一点;△A′BO′、△A′BP′分别由△AOB、△APB逆时针旋转而得,旋转角都为60°,则下列结论:
如图,O是锐角三角形ABC内一点,∠AOB=∠BOC=∠COA=120°,P是△ABC内不同于O的另一点;△A′BO′、△A′BP′分别由△AOB、△APB逆时针旋转而得,旋转角都为60°,则下列结论:①A′O′+O′O=AO+BO.
②A′、O′、O、C在一条直线上.
③A′P′+P′P=PA+PB.
④PA+PB+PC>AO+BO+CO.
其中正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 由于△A′BO′,△A′BP′分别由△AOB,△APB旋转而得,旋转角都为60°,得到BO′=BO,BP′=BP,∠OBO′=∠PBP′=60°,∠A′O′B=∠AOB,O′A′=OA,P′A′=PA,则△BOO′和△BPP′都是等边三角形,得到∠BOO′=∠BO′O=60°,OO′=OB,而∠AOB=∠BOC=∠COA=120°,即可得到四个结论都正确.
解答 解:连PP′,如图,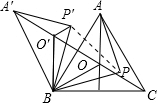
∵△A′BO′,△A′BP′分别由△AOB,△APB旋转而得,旋转角都为60°,
∴BO′=BO,BP′=BP,∠OBO′=∠PBP′=60°,∠A′O′B=∠AOB,O′A′=OA,P′A′=PA,
∴△BOO′和△BPP′都是等边三角形,
∴∠BOO′=∠BO′O=60°,OO′=OB,
∴A′O′+O′O=AO+BO,所以①正确;
而∠AOB=∠BOC=∠COA=120°,
∴∠A′O′O=∠O′OC=180°,
即△O′BO为等边三角形,且A′,O′,O,C在一条直线上,所以②正确;
A′P′+P′P=PA+PB,所以③正确;
又∵CP+PP′+P′A′>CA′=CO+OO′+O′A′,
∴PA+PB+PC>AO+BO+CO,所以④正确.
故选:D.
点评 本题考查了旋转的性质:旋转前后的两个图形全等,对应点与旋转中心的连线段的夹角等于旋转角,对应点到旋转中心的距离相等.也考查了等边三角形的性质以及两点之间线段最短.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.2010年4月14日,青海玉树发生7.1级地震,人民群众的生命财产受到严重损失,社会各界积极为玉树捐献爱心,4月20日央视赈灾晚会共收到社会为玉树捐款21.75亿元,用科学记数法可表示为( )
| A. | 2.175×108元 | B. | 2.175×109元 | C. | 2.175×1010元 | D. | 2.175×1011元 |
19.某校八年级部分学生利用课外活动时间,积极参加篮球定点投篮的训练,训练结束后进行一次测试,记录如下表:
回答下列问题:
(1)测试记录中,篮球定点投篮进球数的众数是4个,中位数是5个.
(2)求本次测试的人均进球数.
| 进球数(个) | 8 | 7 | 6 | 5 | 4 | 3 |
| 人数 | 2 | 2 | 5 | 7 | 9 | 3 |
(1)测试记录中,篮球定点投篮进球数的众数是4个,中位数是5个.
(2)求本次测试的人均进球数.
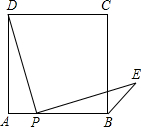 点P是正方形ABCD边AB上一点(不与A、B重合),连接PD并将线段PD绕点P顺时针旋转90°,得线段PE,连接BE,则∠CBE等于45度.
点P是正方形ABCD边AB上一点(不与A、B重合),连接PD并将线段PD绕点P顺时针旋转90°,得线段PE,连接BE,则∠CBE等于45度.