题目内容
6.已知x2-4x+1=0,求x4-x-4的值.分析 先把方程两边除以x可得x+$\frac{1}{x}$=4,再利用完全平方公式可计算出x-$\frac{1}{x}$=±$\sqrt{(x+\frac{1}{x})^{2}-4}$=±2$\sqrt{3}$,则根据平方差公式可计算出x2-$\frac{1}{{x}^{2}}$=±8$\sqrt{3}$,接着根据完全平方公式计算x2+$\frac{1}{{x}^{2}}$=(x+$\frac{1}{x}$)2-2=14,然后根据平方差公式得到x4-x-4=x4-$\frac{1}{{x}^{4}}$=(x2-$\frac{1}{{x}^{2}}$)(x2+$\frac{1}{{x}^{2}}$),再利用整体代入的方法计算.
解答 解:∵x2-4x+1=0,
∴x-4+$\frac{1}{x}$=0,即x+$\frac{1}{x}$=4,
∴x-$\frac{1}{x}$=±$\sqrt{(x-\frac{1}{x})^{2}}$=±$\sqrt{(x+\frac{1}{x})^{2}-4}$=±$\sqrt{{4}^{2}-4}$=±2$\sqrt{3}$,
∴x2-$\frac{1}{{x}^{2}}$=(x+$\frac{1}{x}$)(x-$\frac{1}{x}$)=±8$\sqrt{3}$,
∵x2+$\frac{1}{{x}^{2}}$=(x+$\frac{1}{x}$)2-2=42-2=14,
∴x4-x-4=x4-$\frac{1}{{x}^{4}}$=(x2-$\frac{1}{{x}^{2}}$)(x2+$\frac{1}{{x}^{2}}$)=±8$\sqrt{3}$×14=±112$\sqrt{3}$.
点评 本题考查了一元二次方程的解:能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.本题的关键是熟练掌握完全平方公式.

 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案| A. | $\frac{12}{5}$ | B. | $\frac{4}{25}$ | C. | $\frac{3}{4}$ | D. | $\frac{9}{4}$ |
 如图,AC:BC=5:7,AD:BD=5:11,若CD=11cm,则AB=$\frac{528}{5}$cm.
如图,AC:BC=5:7,AD:BD=5:11,若CD=11cm,则AB=$\frac{528}{5}$cm. 如图,点C在线段AB上,D是线段AC的中点,若BD=5cm,BC=2cm,则AB的长度为8cm.
如图,点C在线段AB上,D是线段AC的中点,若BD=5cm,BC=2cm,则AB的长度为8cm.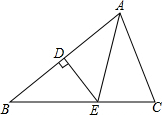 已知,如图,∠ABC中,AB=BC,DE是AB的中垂线,且BE=AC,求证:∠B=∠EAC.
已知,如图,∠ABC中,AB=BC,DE是AB的中垂线,且BE=AC,求证:∠B=∠EAC.