题目内容
11.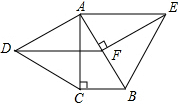 如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°.分别以直角边AC和斜边AB向外作等边△ACD、等边△ABE.过点E,作EF⊥AB,垂足为F,连结DF.
如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°.分别以直角边AC和斜边AB向外作等边△ACD、等边△ABE.过点E,作EF⊥AB,垂足为F,连结DF.求证:
(1)AC=EF;
(2)四边形ADFE是平行四边形.
分析 (1)利用等边三角形的性质得出∠AEF=∠CAB,进而利用AAS求出△AEF≌△BAC,进而得出答案;
(2)根据(1)中所求结合平行线的判定方法得出AD$\stackrel{∥}{=}$EF,即可得出答案.
解答  证明:(1)∵∠BAC=30°,以直角边AB向外作等边△ABE,
证明:(1)∵∠BAC=30°,以直角边AB向外作等边△ABE,
∴∠CAB=∠CAB+∠BAE=90°,AE=AB,
∵EF⊥AB,
∴∠EAF+∠AEF=90°,
∴∠AEF=∠CAB,
在△AEF和△BAC中,
$\left\{\begin{array}{l}{∠AFE=∠ACB}\\{∠AEF=∠CAB}\\{AE=AB}\end{array}\right.$,
∴△AEF≌△BAC(AAS),
∴AC=EF;
(2)∵以直角边AC向外作等边△ACD,∠BAC=30°,
∴∠DAB=90°,AD=AC,
又∵EF⊥AB,
∴AD∥EF,
∵AC=EF,
∴AD=EF,
∴AD$\stackrel{∥}{=}$EF,
∴四边形ADFE是平行四边形.
点评 此题主要考查了全等三角形的判定与性质以及平行四边形的判定等知识,正确利用全等三角形的判定方法是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.下列叙述中错误的是( )
| A. | 两个正方形是相似图形 | |
| B. | 两个菱形是相似图形 | |
| C. | 底角相等的两个等腰三角形是相似图形 | |
| D. | 顶角相等的两个等腰三角形是相似图形 |
19.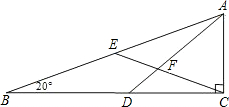 如图,在△ABC中,∠ACB=90°,D在BC上,E是AB的中点,AD、CE相交于F,且AD=DB.若∠B=20°,则∠DFE等于( )
如图,在△ABC中,∠ACB=90°,D在BC上,E是AB的中点,AD、CE相交于F,且AD=DB.若∠B=20°,则∠DFE等于( )
 如图,在△ABC中,∠ACB=90°,D在BC上,E是AB的中点,AD、CE相交于F,且AD=DB.若∠B=20°,则∠DFE等于( )
如图,在△ABC中,∠ACB=90°,D在BC上,E是AB的中点,AD、CE相交于F,且AD=DB.若∠B=20°,则∠DFE等于( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
6.若关于x的一元二次方程(a+1)x2+x+a2-1=0的一个根是0,则这个方程的另一个根是( )
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | 1 | D. | -1 |
 如图,△ABC中,∠B,∠C的平分线交于P,∠A=90°,求∠P.
如图,△ABC中,∠B,∠C的平分线交于P,∠A=90°,求∠P.