题目内容
3.先阅读下列材料:我们已经学过将一个多项式分解因式的方法有提公因式法和运用公式法,其实分解因式的方法还有分组分解法、拆项法、十字相乘法等等.
(1)分组分解法:将一个多项式适当分组后,可提公因式或运用公式继续分解的方法.
如:ax+by+bx+ay=(ax+bx)+(ay+by)
=x(a+b)+y(a+b)
=(a+b)(x+y)
2xy+y2-1+x2
=x2+2xy+y2-1
=(x+y)2-1
=(x+y+1)(x+y-1)
(2)拆项法:将一个多项式的某一项拆成两项后,可提公因式或运用公式继续分解的方法.如:
x2+2x-3
=x2+2x+1-4
=(x+1)2-22
=(x+1+2)(x+1-2)
=(x+3)(x-1)
请你仿照以上方法,探索并解决下列问题:
(1)分解因式:a2-b2+a-b;
(2)分解因式:x2-6x-7;
(3)分解因式:a2+4ab-5b2.
分析 仿照题中的方法,得到十字相乘法的技巧,分别将各项分解即可.
解答 解:(1)原式=(a+b)(a-b)+(a-b)=(a-b)(a+b+1);
(2)原式=(x-7)(x+1);
(3)原式=(a-b)(a+5b).
点评 此题考查了因式分解-十字相乘法,熟练掌握十字相乘法是解本题的关键.

练习册系列答案
相关题目
15.下列分式是最简分式的( )
| A. | $\frac{a+b}{{{a^2}+{b^2}}}$ | B. | $\frac{a}{{{a^2}-3a}}$ | C. | $\frac{2a}{{3{a^2}b}}$ | D. | $\frac{{{a^2}-ab}}{{{a^2}-{b^2}}}$ |
12.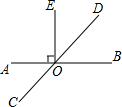 如图,直线AB,CD相交于点O,OE⊥AB于O,若∠BOD=40°,则不正确的结论是( )
如图,直线AB,CD相交于点O,OE⊥AB于O,若∠BOD=40°,则不正确的结论是( )
 如图,直线AB,CD相交于点O,OE⊥AB于O,若∠BOD=40°,则不正确的结论是( )
如图,直线AB,CD相交于点O,OE⊥AB于O,若∠BOD=40°,则不正确的结论是( )| A. | ∠AOC=40° | B. | ∠COE=130° | C. | ∠EOD=40° | D. | ∠BOE=90° |
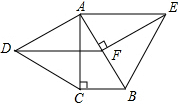 如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°.分别以直角边AC和斜边AB向外作等边△ACD、等边△ABE.过点E,作EF⊥AB,垂足为F,连结DF.
如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°.分别以直角边AC和斜边AB向外作等边△ACD、等边△ABE.过点E,作EF⊥AB,垂足为F,连结DF. 在2011元旦化妆晚会上,学生小明自制了一个无底圆锥形纸帽,如图所示,围成这个纸帽的面积是48πcm2.
在2011元旦化妆晚会上,学生小明自制了一个无底圆锥形纸帽,如图所示,围成这个纸帽的面积是48πcm2.