题目内容
19.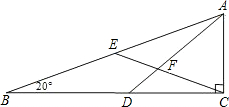 如图,在△ABC中,∠ACB=90°,D在BC上,E是AB的中点,AD、CE相交于F,且AD=DB.若∠B=20°,则∠DFE等于( )
如图,在△ABC中,∠ACB=90°,D在BC上,E是AB的中点,AD、CE相交于F,且AD=DB.若∠B=20°,则∠DFE等于( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
分析 根据直角三角形斜边上中线性质得出BE=CE,根据等腰三角形性质得出∠ECB=∠B=20°,∠DAB=∠B=20°,根据三角形外角性质求出∠ADC=∠B+∠DAB=40°,根据∠三角形外角性质得出DFE=∠ADC+∠ECB,代入求出即可.
解答 解:∵在△ABC中,∠ACB=90°,E是AB的中点,
∴BE=CE,
∵∠B=20°
∴∠ECB=∠B=20°,
∵AD=BD,∠B=20°,
∴∠DAB=∠B=20°,
∴∠ADC=∠B+∠DAB=20°+20°=40°,
∴∠DFE=∠ADC+∠ECB=40°+20°=60°,
故选D.
点评 本题考查了等腰三角形的性质,三角形外角性质,直角三角形斜边上中线性质的应用,能求出∠ADC和∠ECB的度数是解此题的关键,注意:直角三角形斜边上的中线等于斜边的一半.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
9.在实数:3.1415926,$\root{3}{64}$,1.010010001,4.$\stackrel{..}{21}$,π,$\frac{22}{7}$中,无理数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
10.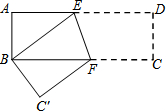 将矩形纸片ABCD按如图方式折叠,使点D与点B重合,点C落在点C′处.折痕为EF,若S△ABE:S四边形ABFE=4:9,则cos∠BEF=( )
将矩形纸片ABCD按如图方式折叠,使点D与点B重合,点C落在点C′处.折痕为EF,若S△ABE:S四边形ABFE=4:9,则cos∠BEF=( )
 将矩形纸片ABCD按如图方式折叠,使点D与点B重合,点C落在点C′处.折痕为EF,若S△ABE:S四边形ABFE=4:9,则cos∠BEF=( )
将矩形纸片ABCD按如图方式折叠,使点D与点B重合,点C落在点C′处.折痕为EF,若S△ABE:S四边形ABFE=4:9,则cos∠BEF=( )| A. | $\frac{1}{3}$ | B. | $\frac{3\sqrt{10}}{10}$ | C. | 3 | D. | $\frac{\sqrt{10}}{10}$ |
7.计算$\frac{1}{5}+({-\frac{1}{2}})$的值是( )
| A. | $\frac{1}{3}$ | B. | -$\frac{3}{10}$ | C. | 3 | D. | -3 |
9.估计$\sqrt{27}$×$\sqrt{\frac{1}{3}}$$+\sqrt{20}$的运算结果应在( )
| A. | 5到6之间 | B. | 6到7之间 | C. | 7到8之间 | D. | 8到9之间 |
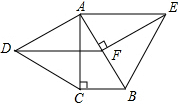 如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°.分别以直角边AC和斜边AB向外作等边△ACD、等边△ABE.过点E,作EF⊥AB,垂足为F,连结DF.
如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°.分别以直角边AC和斜边AB向外作等边△ACD、等边△ABE.过点E,作EF⊥AB,垂足为F,连结DF.