题目内容
6．若关于x的一元二次方程（a+1）x2+x+a2-1=0的一个根是0，则这个方程的另一个根是（ ）| A． | $\frac{1}{2}$ | B． | $-\frac{1}{2}$ | C． | 1 | D． | -1 |
分析 根据一元二次方程的解的定义，将x=0代入原方程求得a的值，然后通过根与系数的关系x1•x2=$\frac{c}{a}$求得方程的另一个根．
解答 解：根据题意，得
a2-1=0，且a+1≠0
解得a=1；
设关于x的一元二次方程2x2-x+a=0的另一个根为x2，
则0+x2=-$\frac{1}{2}$，
解得x2=-$\frac{1}{2}$．
故选B．
点评 本题考查了一元二次方程的解的定义．解答关于x的一元二次方程2x2-x+a=0的另一个根时，也可以直接利用根与系数的关系x1+x2=-$\frac{b}{a}$解答．
练习册系列答案
相关题目
17．如图是由若干个全等的等腰梯形拼成的四边形，四边形的周长与梯形的个数如表中所列，观察图形并思考当这个等腰梯形共有55个时，所拼成的图形的周长为（ ） 
| 梯形个数 | 1 | 2 | 3 | … |
| 图形周长 | 5a | 8a | 11a | … |
| A． | 167a | B． | 166a | C． | 165a | D． | 164a |
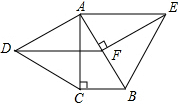如图，在Rt△ABC中，∠ACB=90°，∠BAC=30°．分别以直角边AC和斜边AB向外作等边△ACD、等边△ABE．过点E，作EF⊥AB，垂足为F，连结DF．
15．下列分式是最简分式的（ ）
| A． | $\frac{a+b}{{{a^2}+{b^2}}}$ | B． | $\frac{a}{{{a^2}-3a}}$ | C． | $\frac{2a}{{3{a^2}b}}$ | D． | $\frac{{{a^2}-ab}}{{{a^2}-{b^2}}}$ |
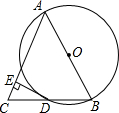如图，△ABC中，AB=AC，以AB为直径的⊙O交BC于点D，过点D作DE⊥AC，垂足为E．