题目内容
11.某单位招聘员工,采取笔试与面试相结合的方式进行,两项成绩的原始分均为100分.前5名选手的得分如下:| 序号项目 | 1 | 2 | 3 | 4 | 5 |
| 笔试成绩/分 | 85 | 84 | 84 | 90 | 80 |
| 面试成绩/分 | 90 | 86 | 80 | 90 | 85 |
(1)这5名选手笔试成绩的中位数是84分,众数是84分.
(2)现得知1号、2号、3号选手的综合成绩分别为88分、85.2分、81.6分,求出其余两名选手的综合成绩,并确定谁将被录取?
分析 (1)根据中位数和众数的定义即把这组数据从小到大排列,再找出最中间的数就是中位数,然后找出出现的次数最多的数即是众数;
(2)设笔试成绩和面试成绩各占的百分比是x,y,根据1号笔试成绩和面试成绩,求出各自所占的百分比,从而求出4号和5号的成绩,再进行比较即可.
解答 解:(1)把这组数据从小到大排列为,80,84,84,85,90,最中间的数是84分,
则这5名选手笔试成绩的中位数是84分,
84出现了2次,出现的次数最多,
则这5名选手笔试成绩的众数是84分;
故答案为:84分,84分;
(2)设笔试成绩和面试成绩各占的百分比是x,y,根据题意得:
$\left\{\begin{array}{l}{x+y=1}\\{85x+90y=88}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=0.4}\\{y=0.6}\end{array}\right.$,
则笔试成绩和面试成绩各占的百分比是40%,60%;
4号选手的综合成绩是90×0.4+90×0.6=90(分),
5号选手的综合成绩是80×0.4+85×0.6=83(分),
则4号将被录取.
点评 此题考查了加权平均数,用到的知识点是中位数、众数、加权平均数的计算公式,关键灵活运用有关知识列出算式.

练习册系列答案
相关题目
9.下列各图中,表示数轴的是( )
| A. |  | B. |  | ||
| C. |  | D. |  |
7.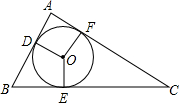 如图,⊙O是△ABC的内切圆.切点分别为D、E、F,若∠DOE=120°,∠EOF=150°,则△ABC的3个内角的度数依次为( )
如图,⊙O是△ABC的内切圆.切点分别为D、E、F,若∠DOE=120°,∠EOF=150°,则△ABC的3个内角的度数依次为( )
 如图,⊙O是△ABC的内切圆.切点分别为D、E、F,若∠DOE=120°,∠EOF=150°,则△ABC的3个内角的度数依次为( )
如图,⊙O是△ABC的内切圆.切点分别为D、E、F,若∠DOE=120°,∠EOF=150°,则△ABC的3个内角的度数依次为( )| A. | 90°,60°,30° | B. | 80°,60°,40° | C. | 90°,50°,40° | D. | 80°,70°,30° |
16. 如图,直角三角形ABC中,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P、Q两点分别在AC和AC的垂线AX上移动,当△ABC和△APQ全等时,AP长度为( )
如图,直角三角形ABC中,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P、Q两点分别在AC和AC的垂线AX上移动,当△ABC和△APQ全等时,AP长度为( )
 如图,直角三角形ABC中,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P、Q两点分别在AC和AC的垂线AX上移动,当△ABC和△APQ全等时,AP长度为( )
如图,直角三角形ABC中,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P、Q两点分别在AC和AC的垂线AX上移动,当△ABC和△APQ全等时,AP长度为( )| A. | 5cm | B. | 10cm | C. | 5cm或10cm | D. | 不存在 |
1.下列运算正确的是( )
| A. | 4$\sqrt{3}$-3$\sqrt{3}$=1 | B. | $\sqrt{2}$$+\sqrt{3}$=$\sqrt{5}$ | C. | $\frac{\sqrt{8}}{\sqrt{2}}$=2 | D. | $\sqrt{(-3)^{2}}$=-3 |
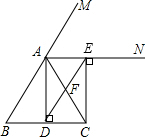 如图,在△ABC中,AB=AC,AD⊥BC垂足为D,AN平分∠CAM,CE⊥AN垂足为E,连接DE交AC于F.
如图,在△ABC中,AB=AC,AD⊥BC垂足为D,AN平分∠CAM,CE⊥AN垂足为E,连接DE交AC于F.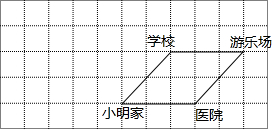 位于汉江沿岸的小明家、学校、医院、游乐场的平面图如图所示.
位于汉江沿岸的小明家、学校、医院、游乐场的平面图如图所示.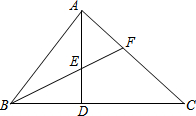 在直角△ABC中,∠BAC=90°,BF平分∠ABC,∠AEF=∠AFE.
在直角△ABC中,∠BAC=90°,BF平分∠ABC,∠AEF=∠AFE. 如图,在Rt△ABC中,斜边AB=5,直角边BC=$\sqrt{5}$,求三角形的面积.
如图,在Rt△ABC中,斜边AB=5,直角边BC=$\sqrt{5}$,求三角形的面积.