题目内容
16.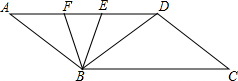 如图,AD∥BC,BE平分∠ABC交AD于点E,BD平分∠EBC.
如图,AD∥BC,BE平分∠ABC交AD于点E,BD平分∠EBC.(1)若∠DBC=30°,求∠A的度数;
(2)若点F在线段AE上,且7∠DBC-2∠ABF=180°,请问图中是否存在与∠DFB相等的角?若存在,请写出这个角,并说明理由;若不存在,请说明理由.
分析 (1)根据角平分线的定义得到∠EBC=2∠DBC=60°,∠ABC=2∠EBC=120°,根据平行线的性质得到∠A+∠ABC=180°,于是得到结论;
(2)设∠DBC=x°,则∠ABC=2∠ABE=(4x)°,根据已知条件得到∠ABF=($\frac{7}{2}$x-90)°,求得∠DBF=(90-$\frac{1}{2}$x)°,根据平行线的性质得到∠DFB+∠CBF=180°,于是得到∠DFB=(90-$\frac{1}{2}$x)°,即可得到结论.
解答 解:(1)∵BD平分∠EBC,∠DBC=30°,
∴∠EBC=2∠DBC=60°,
∵BE平分∠ABC,
∴∠ABC=2∠EBC=120°,
∵AD∥BC,
∴∠A+∠ABC=180°,
∴∠A=60°;
(2)存在∠DFB=∠DBF,
设∠DBC=x°,则∠ABC=2∠ABE=(4x)°,
∵7∠DBC-2∠ABF=180°,
∴7x-2∠ABF=180°,
∴∠ABF=($\frac{7}{2}$x-90)°,
∴∠CBF=∠ABC-∠ABF=($\frac{1}{2}$x+90)°,
∠DBF=∠ABC-∠ABF-∠DBC=(90-$\frac{1}{2}$x)°,
∵AD∥BC,
∴∠DFB+∠CBF=180°,
∴∠DFB=(90-$\frac{1}{2}$x)°,
∴∠DFB=∠DBF.
点评 本题考查了平行线的性质,角平分线的定义,熟练掌握平行线的性质是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.对于反比例函数y=-$\frac{3}{x}$,下列说法正确的是( )
| A. | y随x增大而增大 | |
| B. | 图象在第一、三象限 | |
| C. | 当x的绝对值无限增大时,图象能够与x轴相交 | |
| D. | 图象既是轴对称图形又是中心对称图形 |
8. 如图,点O在直线AB上,且OC⊥OD.若么∠BOD=55°,则∠COA的度数是( )
如图,点O在直线AB上,且OC⊥OD.若么∠BOD=55°,则∠COA的度数是( )
 如图,点O在直线AB上,且OC⊥OD.若么∠BOD=55°,则∠COA的度数是( )
如图,点O在直线AB上,且OC⊥OD.若么∠BOD=55°,则∠COA的度数是( )| A. | 25° | B. | 35° | C. | 45° | D. | 55° |
6.在下列长度的各组线段中,不能构成直角三角形的是( )
| A. | 3,4,5 | B. | $\sqrt{5}$,$\sqrt{12}$,$\sqrt{13}$ | C. | 1,$\sqrt{3}$,2 | D. | 4,5,$\sqrt{41}$ |
 如图,E、F是?ABCD对角线BD上的两点,若要使四边形AECF是平行四边形.则可以添加一个条件是:BE=DF(答案不唯一);.
如图,E、F是?ABCD对角线BD上的两点,若要使四边形AECF是平行四边形.则可以添加一个条件是:BE=DF(答案不唯一);.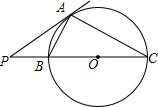 如图,PA是⊙O的切线,割线PBC与⊙O相交于点B、C,PA=6、PB=4,则BC=5.$\frac{AB}{AC}$的值为$\frac{2}{3}$.
如图,PA是⊙O的切线,割线PBC与⊙O相交于点B、C,PA=6、PB=4,则BC=5.$\frac{AB}{AC}$的值为$\frac{2}{3}$.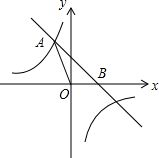 如图,直线y=-x+b与反比例函数$y=-\frac{3}{x}$的图象相交于点A(a,3),且与x轴相交于点B.
如图,直线y=-x+b与反比例函数$y=-\frac{3}{x}$的图象相交于点A(a,3),且与x轴相交于点B.