题目内容
7.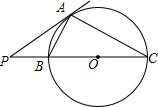 如图,PA是⊙O的切线,割线PBC与⊙O相交于点B、C,PA=6、PB=4,则BC=5.$\frac{AB}{AC}$的值为$\frac{2}{3}$.
如图,PA是⊙O的切线,割线PBC与⊙O相交于点B、C,PA=6、PB=4,则BC=5.$\frac{AB}{AC}$的值为$\frac{2}{3}$.
分析 连接OA,只要证明△APB∽△CPA,即可得到$\frac{PA}{PC}$=$\frac{PB}{PA}$=$\frac{AB}{AC}$,由此可以解决问题.
解答  解:连接OA,
解:连接OA,
∵PA是切线,
∴PA⊥OA,
∴∠PAO=90°,
∴∠PAB+∠OAB=90°,
∵OA=OB,
∴∠OAB=∠OBA,
∴∠C+∠OBA=90°,
∴∠PAB=∠C,∵∠APB=∠APC,
∴△APB∽△CPA,
∴$\frac{PA}{PC}$=$\frac{PB}{PA}$=$\frac{AB}{AC}$,
∵PA=6,PB=4,
∴PC=9,BC=PC-PB=5,
∴$\frac{AB}{AC}$=$\frac{PA}{PC}$=$\frac{6}{9}$=$\frac{2}{3}$.
故答案分别为5,$\frac{2}{3}$.
点评 本题考查切线的性质、相似三角形的判定和性质等知识,解题的关键是正确寻找相似三角形,路相似三角形的性质解决问题,属于中考常考题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.从方程组$\left\{\begin{array}{l}{x={m}^{2}-1}\\{y=5{m}^{2}+4}\end{array}\right.$中得出x与y的关系是( )
| A. | y=5x+1 | B. | y=5x+9 | C. | y=$\frac{1}{5}$x-$\frac{9}{5}$ | D. | y=$\frac{1}{5}$x+$\frac{1}{5}$ |
17.已知关于x的一元二次方程x2+x+m2-1=0的一个根是0,则m的值为( )
| A. | 1 | B. | 0 | C. | -1 | D. | 1或-1 |
 如图,以?ABCD的一边为直径⊙O,恰好与边CD相切于点D,E是⊙O上一点,点E与点D位于直径AB的两侧.
如图,以?ABCD的一边为直径⊙O,恰好与边CD相切于点D,E是⊙O上一点,点E与点D位于直径AB的两侧. 如图,正方形ABCD中,E为对角线AC上一点,连结EB、ED,延长BE交AD于点F.
如图,正方形ABCD中,E为对角线AC上一点,连结EB、ED,延长BE交AD于点F.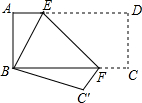 如图所示,将长方形纸片ABCD折叠,使点D与点B重合,点C落在点C′处,折痕为EF,若∠EFC′=125°,那么∠AEB的度数是70°.
如图所示,将长方形纸片ABCD折叠,使点D与点B重合,点C落在点C′处,折痕为EF,若∠EFC′=125°,那么∠AEB的度数是70°.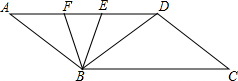 如图,AD∥BC,BE平分∠ABC交AD于点E,BD平分∠EBC.
如图,AD∥BC,BE平分∠ABC交AD于点E,BD平分∠EBC.