题目内容
4.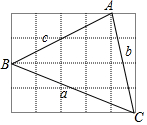 如图所示,在正方形网格中,每个小正方形的边长为1,则网格上的△ABC(△ABC的各项点均在格点上)的三边a、b、c之间的大小关系是( )
如图所示,在正方形网格中,每个小正方形的边长为1,则网格上的△ABC(△ABC的各项点均在格点上)的三边a、b、c之间的大小关系是( )| A. | c<a<b | B. | b<c<a | C. | c<b<a | D. | a<c<b |
分析 先根据勾股定理求出a、b、c的值,再比较大小即可.
解答 解:由题意可知,a=$\sqrt{{2}^{2}+{5}^{2}}$=$\sqrt{29}$,b=$\sqrt{{1}^{2}+{4}^{2}}$=$\sqrt{17}$,c=$\sqrt{{2}^{2}+{4}^{2}}$=$\sqrt{20}$,
∵$\sqrt{17}$<$\sqrt{20}$<$\sqrt{29}$,
∴b<c<a.
故选B.
点评 本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.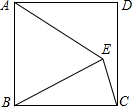 如图,以正方形ABCD的边AB为一边向内作等边△ABE,连结EC,则∠AEC的度数为( )
如图,以正方形ABCD的边AB为一边向内作等边△ABE,连结EC,则∠AEC的度数为( )
 如图,以正方形ABCD的边AB为一边向内作等边△ABE,连结EC,则∠AEC的度数为( )
如图,以正方形ABCD的边AB为一边向内作等边△ABE,连结EC,则∠AEC的度数为( )| A. | 120° | B. | 135° | C. | 145° | D. | 150° |
12.从一个多边形的一个顶点出发,可以画出7条对角线,则这个多边形的边数为( )
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
19.已知点A、B的坐标分别为(1,0)、(2,0).若顶点在x轴下方的二次函数y=x2+(a-3)x+3的图象与线段AB恰好只有一个交点,则a的取值范围( )
| A. | $-1≤a<-\frac{1}{2}$ | B. | $-1≤a≤\frac{1}{2}$ | C. | $\frac{1}{2}<a<2$ | D. | -1<a≤1 |
16.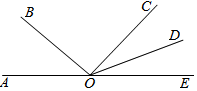 如图,点A、O、E在同一直线上,∠AOB=40°,∠EOD=28°46′,OD平分∠COE,则∠COB的度数为( )
如图,点A、O、E在同一直线上,∠AOB=40°,∠EOD=28°46′,OD平分∠COE,则∠COB的度数为( )
 如图,点A、O、E在同一直线上,∠AOB=40°,∠EOD=28°46′,OD平分∠COE,则∠COB的度数为( )
如图,点A、O、E在同一直线上,∠AOB=40°,∠EOD=28°46′,OD平分∠COE,则∠COB的度数为( )| A. | 57°32′ | B. | 82°28′ | C. | 111°14′ | D. | 125°37′ |
14. 已知有理数a、b、c在数轴上的位置如图所示,下列子正确的是( )
已知有理数a、b、c在数轴上的位置如图所示,下列子正确的是( )
 已知有理数a、b、c在数轴上的位置如图所示,下列子正确的是( )
已知有理数a、b、c在数轴上的位置如图所示,下列子正确的是( )| A. | cb>ab | B. | ac>ab | C. | cb<ab | D. | c+b>a+b |
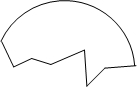 一个破圆轮残片如图所示,现要修复该圆轮,怎样确定这个圆轮残片的圆心和半径?(写出找圆心和半径的步骤)
一个破圆轮残片如图所示,现要修复该圆轮,怎样确定这个圆轮残片的圆心和半径?(写出找圆心和半径的步骤) 已知在△ABC中,AB=AC=5,BC=6,AD是BC边上的中线,四边形ADBE是平行四边形.
已知在△ABC中,AB=AC=5,BC=6,AD是BC边上的中线,四边形ADBE是平行四边形.