题目内容
8．
如图，下列条件中，能判断AB∥CD的是（ ）| A． | ∠1=∠2 | B． | ∠3=∠4 | C． | ∠BAC=∠BCD | D． | ∠ABC+∠BAD=180° |
分析 根据内错角相等，两直线平行；同旁内角互补，两直线平行；同位角相等，两直线平行进行判断即可．
解答 解：A、由∠1=∠2，能判定AD∥CB，故A选项不合题意；
B、由∠3=∠4，可证AB∥DC，故B选项符合题意；
C、由∠BAC=∠BCD，不能判断AB∥CD，故C选项不合题意；
D、由∠ABC+∠BAD=180°，可证AD∥CB，故D选项不合题意．
故选：B．
点评 本题主要考查了平行线的判定的运用，解题时注意：内错角相等，两直线平行；同旁内角互补，两直线平行；同位角相等，两直线平行．
练习册系列答案
相关题目
19．已知点A、B的坐标分别为（1，0）、（2，0）．若顶点在x轴下方的二次函数y=x2+（a-3）x+3的图象与线段AB恰好只有一个交点，则a的取值范围（ ）
| A． | $-1≤a＜-\frac{1}{2}$ | B． | $-1≤a≤\frac{1}{2}$ | C． | $\frac{1}{2}＜a＜2$ | D． | -1＜a≤1 |
16．
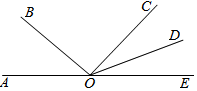如图，点A、O、E在同一直线上，∠AOB=40°，∠EOD=28°46′，OD平分∠COE，则∠COB的度数为（ ）
如图，点A、O、E在同一直线上，∠AOB=40°，∠EOD=28°46′，OD平分∠COE，则∠COB的度数为（ ）| A． | 57°32′ | B． | 82°28′ | C． | 111°14′ | D． | 125°37′ |
3．
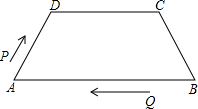如图，在等腰梯形ABCD中，AB∥DC，AD=BC=5，DC=7，AB=13，点P从点A出发，以3个单位/s的速度沿AD→DC向终点C运动，同时点Q从点B出发，以1个单位/s的速度沿BA向终点A运动，在运动期间，当四边形PQBC为平行四边形时，运动时间为（ ）
如图，在等腰梯形ABCD中，AB∥DC，AD=BC=5，DC=7，AB=13，点P从点A出发，以3个单位/s的速度沿AD→DC向终点C运动，同时点Q从点B出发，以1个单位/s的速度沿BA向终点A运动，在运动期间，当四边形PQBC为平行四边形时，运动时间为（ ）| A． | 4s | B． | 3 s | C． | 2 s | D． | 1s |
已知在△ABC中，AB=AC=5，BC=6，AD是BC边上的中线，四边形ADBE是平行四边形．
20．下列说法中错误的是（ ）
| A． | 不等式x+1≤4的整数解有无数个 | B． | 不等式x+4＜5的解集是x＜1 | ||
| C． | 不等式x＜4的正整数解为有限个 | D． | 0是不等式3x＜-1的解 |