题目内容
6.观察下列等式:$\frac{1}{1×2}$=1-$\frac{1}{2}$;
$\frac{1}{2×3}$=$\frac{1}{2}$-$\frac{1}{3}$;
$\frac{1}{3×4}$=$\frac{1}{3}$-$\frac{1}{4}$…
(1)请直接写出$\frac{1}{n}$-$\frac{1}{n+1}$的结果,并证明这个等式.
(2)根据(1)中的等式计算:
①$\frac{13}{143}$-$\frac{13}{144}$;
②$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{99×100}$;
(3)先化简,再求值:$\frac{100}{1×2}$+$\frac{100}{2×3}$+$\frac{100}{3×4}$+…$\frac{100}{n(n+1)}$,其中n=999.
分析 (1)通过前面的等式的特点,直接得到结果,利用分式的加减证明结论;
(2)利用等式的变形计算各题;
(3)提出100后,利用(1)的结论代入求值.
解答 解:(1)$\frac{1}{n}$-$\frac{1}{n+1}$=$\frac{1}{n(n+1)}$.
证明:$\frac{1}{n}$-$\frac{1}{n+1}$
=$\frac{n+1}{n(n+1)}-\frac{n}{n(n+1)}$
=$\frac{1}{n(n+1)}$.
(2)
①$\frac{13}{143}$-$\frac{13}{144}$
=13($\frac{1}{143}-\frac{1}{144}$)
=13×$\frac{1}{143×144}$
=$\frac{1}{1584}$;
②$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{99×100}$
=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}-\frac{1}{4}$+…+$\frac{1}{99}-\frac{1}{100}$
=1-$\frac{1}{100}$
=$\frac{99}{100}$.
(3)$\frac{100}{1×2}$+$\frac{100}{2×3}$+$\frac{100}{3×4}$+…$\frac{100}{n(n+1)}$
=100($\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{n(n+1)}$)
=100(1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}-\frac{1}{4}$+…+$\frac{1}{n}-\frac{1}{n+1}$)
=100(1-$\frac{1}{n+1}$)
=$\frac{100n}{n+1}$
当n=999时,原式=$\frac{999×100}{999+1}$
=$\frac{999}{10}$.
点评 本题考查了等式变形及应用.灵活运用$\frac{1}{n}$-$\frac{1}{n+1}$=$\frac{1}{n(n+1)}$是解决本题的关键.

 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案| A. | -3 | B. | 3.14 | C. | $\frac{22}{7}$ | D. | $\sqrt{8}$ |
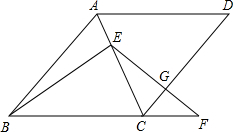 在菱形ABCD中,点E在对角线AC上,点F在BC的延长线上,EF=EB,EF与CD相交于点G.
在菱形ABCD中,点E在对角线AC上,点F在BC的延长线上,EF=EB,EF与CD相交于点G. 如图,长方形纸片ABCD中,AB=3,AD=9,将此长方形纸片折叠,使点D与点B重合,折痕为EF,求△BEF的面积为:7.5.
如图,长方形纸片ABCD中,AB=3,AD=9,将此长方形纸片折叠,使点D与点B重合,折痕为EF,求△BEF的面积为:7.5.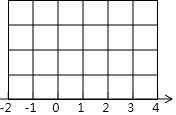 如图,每个小格的顶点叫做格点,每个小正方形边长为1,
如图,每个小格的顶点叫做格点,每个小正方形边长为1, 如图,?ABCD的对角线AC、BD相交于点O,若AB=5cm,BC=7cm,△COD的周长是17cm,则△BOC的周长是19cm.
如图,?ABCD的对角线AC、BD相交于点O,若AB=5cm,BC=7cm,△COD的周长是17cm,则△BOC的周长是19cm.
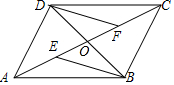 如图,四边形ABCD的对角线AC、BD相交于点O,且O是AC的中点,AE=CF,DF∥BE.
如图,四边形ABCD的对角线AC、BD相交于点O,且O是AC的中点,AE=CF,DF∥BE.