题目内容
14. 如图,长方形纸片ABCD中,AB=3,AD=9,将此长方形纸片折叠,使点D与点B重合,折痕为EF,求△BEF的面积为:7.5.
如图,长方形纸片ABCD中,AB=3,AD=9,将此长方形纸片折叠,使点D与点B重合,折痕为EF,求△BEF的面积为:7.5.
分析 由将此长方形纸片折叠,使点D与点B重合,折痕为EF,易得△BEF是等腰三角形,即BE=BF=DE,然后设BF=x,由勾股定理得方程32+(9-x)2=x2,继而求得答案.
解答 解:∵长方形纸片ABCD中,AD∥BC,
∴∠DEF=∠BFE,
∵将此长方形纸片折叠,使点D与点B重合,折痕为EF,
∴BE=DE,∠DEF=∠BEF,
∴∠BEF=∠BFE,
∴BE=BF,
设BF=x,则BE=DE=BF=x,
∵AB=3,AD=9,
∴AE=AD-DE=x-9,
在Rt△ABE中,AB2+AE2=BE2,
∴32+(9-x)2=x2,
解得:x=5,
∴S△BEF=$\frac{1}{2}$BF•AB=$\frac{1}{2}$×5×3=7.5.
故答案为:7.5.
点评 此题考查了折叠的性质、矩形的性质以及勾股定理的应用.注意利用方程思想求解是关键.

练习册系列答案
相关题目
12.下列方程中是关于x的一元二次方程的是( )
| A. | (x-1)(x+2)=1 | B. | 3x2-2xy-5y2=0 | C. | x2+$\frac{1}{{x}^{2}}$=0 | D. | ax2+bx+c=0 |
9.为了了解500名初三毕业班学生一分钟跳绳次数的情况,某校抽取了一部分初三毕业生进行一分钟跳绳次数的测试,将所得数据进行处理,可得频率分布表:
(1)这个问题中,总体是初三毕业班500名学生一分钟跳绳次数的情况的全体; 样本容量a=100;
(2)第四小组的频数b=39,频率c=0.39;
(3)若次数在110次(含110次)以上为达标,试估计该校初三毕业生一分钟跳绳的达标的人数是多少?
(1)这个问题中,总体是初三毕业班500名学生一分钟跳绳次数的情况的全体; 样本容量a=100;
(2)第四小组的频数b=39,频率c=0.39;
(3)若次数在110次(含110次)以上为达标,试估计该校初三毕业生一分钟跳绳的达标的人数是多少?
| 组别 | 分 组 | 频数 | 频率 |
| 1 | 89.5~99.5 | 4 | 0.04 |
| 2 | 99.5~109.5 | 3 | 0.03 |
| 3 | 109.5~119.5 | 46 | 0.46 |
| 4 | 119.5~129.5 | b | c |
| 5 | 129.5~139.5 | 6 | 0.06 |
| 6 | 139.5~149.5 | 2 | 0.02 |
| 合 计 | a | 1.00 | |
3.下列各式从左到右是分解因式的是( )
| A. | 10x3y4=2xy•5x2y3 | B. | 4a2-4ab+b2=(2a-b)2 | ||
| C. | (a-b)(a+b)=a2-b2 | D. | x2+3x-5=(x-1)(x+4)-1 |
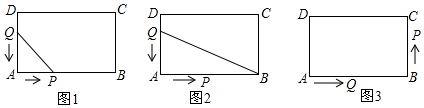
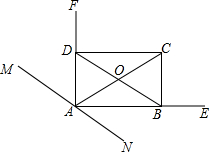 如图所示,AF是∠MAC角平分线,AE是∠NAC的角平分线,OB=OD,且OA=OC,求证:四边形ABCD为矩形.
如图所示,AF是∠MAC角平分线,AE是∠NAC的角平分线,OB=OD,且OA=OC,求证:四边形ABCD为矩形.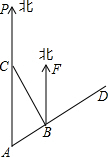 如图,我军两艘巡洋舰在南海某海域执行巡逻任务,两舰自A处沿AD方向航行,巡逻到B处后,1号舰沿原来的方向继续前行,2号舰则沿北偏西方向航行到C处(C在A的正北方向)后改变航线,计划沿与1号舰航线平行,且方向相同的路线航行.
如图,我军两艘巡洋舰在南海某海域执行巡逻任务,两舰自A处沿AD方向航行,巡逻到B处后,1号舰沿原来的方向继续前行,2号舰则沿北偏西方向航行到C处(C在A的正北方向)后改变航线,计划沿与1号舰航线平行,且方向相同的路线航行.