题目内容
16.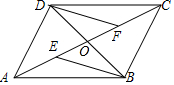 如图,四边形ABCD的对角线AC、BD相交于点O,且O是AC的中点,AE=CF,DF∥BE.
如图,四边形ABCD的对角线AC、BD相交于点O,且O是AC的中点,AE=CF,DF∥BE.(1)求证:△BOE≌△DOF;
(2)求证:四边形ABCD是平行四边形;
(3)当OD与AC满足怎样的数量关系时,四边形ABCD是矩形?并说明理由.
分析 (1)根据AAS或ASA即可证明;
(2)只要证明OD=OB,OA=OC即可解决问题.
(3)根据对角线相等的四边形是矩形即可解决问题;
解答 (1)证明:∵点O是AC中点,
∴OA=OC,
∵AE=CF,
∴OE=OF,
∵DF∥BE,
∴∠OEB=∠OFE,
在△BOE和△DOF中
$\left\{\begin{array}{l}{∠OEB=∠OFD}\\{∠BOE=∠DOF}\\{OE=OF}\end{array}\right.$,
∴△BOE≌△DOF,
(2)∵△BOE≌△DOF,
∴OD=OB,∵OA=OC,
∴四边形ABCD是平行四边形.
(3)结论:当OD=$\frac{1}{2}$AC时,四边形ABCD是矩形.
理由:∵OD=$\frac{1}{2}$AC,OD=OB,
∴BD=AC,
∵四边形ABCD是平行四边形,
∴四边形ABCD是矩形.
点评 此题是平行四边形的判定,主要考查了线段的中点,平行线的性质,全等三角形的判定和性质,解本题的关键是判断△BOE≌△DOF.

练习册系列答案
相关题目
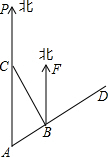 如图,我军两艘巡洋舰在南海某海域执行巡逻任务,两舰自A处沿AD方向航行,巡逻到B处后,1号舰沿原来的方向继续前行,2号舰则沿北偏西方向航行到C处(C在A的正北方向)后改变航线,计划沿与1号舰航线平行,且方向相同的路线航行.
如图,我军两艘巡洋舰在南海某海域执行巡逻任务,两舰自A处沿AD方向航行,巡逻到B处后,1号舰沿原来的方向继续前行,2号舰则沿北偏西方向航行到C处(C在A的正北方向)后改变航线,计划沿与1号舰航线平行,且方向相同的路线航行.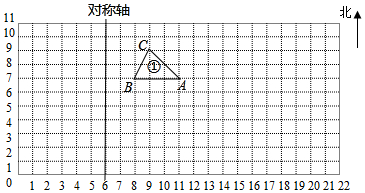 如图每个小正方形的边长表示1厘米,请按要求画图形.
如图每个小正方形的边长表示1厘米,请按要求画图形. 已知:如图,平行四边形ABCD的对角线相交于点O,点E在边BC的延长线上,且OE=OB,联结DE.
已知:如图,平行四边形ABCD的对角线相交于点O,点E在边BC的延长线上,且OE=OB,联结DE.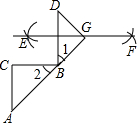 如图,在△ABC中,∠C=90°,DB⊥BC于点B,分别以点D和点B为圆心,以大于$\frac{1}{2}$DB的长为半径作弧,两弧相交于点E和点F,作直线EF,延长AB于点G,连接DG,下面是说明∠A=∠D的说理过程,请把下面的说理过程补充完整:
如图,在△ABC中,∠C=90°,DB⊥BC于点B,分别以点D和点B为圆心,以大于$\frac{1}{2}$DB的长为半径作弧,两弧相交于点E和点F,作直线EF,延长AB于点G,连接DG,下面是说明∠A=∠D的说理过程,请把下面的说理过程补充完整: