题目内容
3.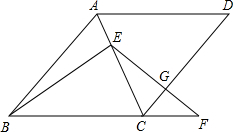 在菱形ABCD中,点E在对角线AC上,点F在BC的延长线上,EF=EB,EF与CD相交于点G.
在菱形ABCD中,点E在对角线AC上,点F在BC的延长线上,EF=EB,EF与CD相交于点G.求证:EG•GF=CG•GD.
分析 想办法证明△DGE∽△FGC,可得$\frac{EG}{CG}$=$\frac{GD}{GF}$,即可解决问题.
解答 证明:连接ED,
∵点E在菱形ABCD的对角线AC上,
∴∠ECB=∠ECD,
∵BC=CD,CE=CE,
∴△BCE≌△DCE,
∴∠EDC=∠EBC,
∵EB=EF,
∴∠EBC=∠EFC,
∴∠EDC=∠EFC,
∵∠DGE=∠FGC,
∴△DGE∽△FGC,
∴$\frac{EG}{CG}$=$\frac{GD}{GF}$,
∴EG•GF=CG•GD;
点评 本题考查全等三角形的判定和性质、相似三角形的判定和性质等知识,解题的关键是正确寻找相似三角形解决问题,属于中考常考题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.某种细胞的直径是0.00000089米,将0.00000089用科学记数法表示为( )
| A. | 89×10-8 | B. | 8.9×10-8 | C. | 0.89×10-7 | D. | 8.9×10-7 |
12.下列方程中是关于x的一元二次方程的是( )
| A. | (x-1)(x+2)=1 | B. | 3x2-2xy-5y2=0 | C. | x2+$\frac{1}{{x}^{2}}$=0 | D. | ax2+bx+c=0 |
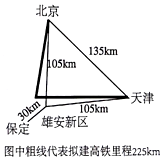 “雄安新区”是中共中央作出“千年大计、国家大事”的重大决策,雄安新区位于北京、天津和保定构成的一个等边三角形腹地,距离北京、天津和保定市分别约105公里、105公里、30公里,如图所示.现拟一列高铁列车从北京经雄安新区到天津比北京与天津的城际特快列车还少用25分,已知高铁速度是城际特快列车的速度2.5倍,高铁列车行驶的里程为225km,北京与天津的里程为135km,求城际特快列车的速度是多少km/h?
“雄安新区”是中共中央作出“千年大计、国家大事”的重大决策,雄安新区位于北京、天津和保定构成的一个等边三角形腹地,距离北京、天津和保定市分别约105公里、105公里、30公里,如图所示.现拟一列高铁列车从北京经雄安新区到天津比北京与天津的城际特快列车还少用25分,已知高铁速度是城际特快列车的速度2.5倍,高铁列车行驶的里程为225km,北京与天津的里程为135km,求城际特快列车的速度是多少km/h? 如图:在2×2正方形网格中,以格点为顶点的△ABC,则sin∠ABC=$\frac{\sqrt{5}}{5}$.
如图:在2×2正方形网格中,以格点为顶点的△ABC,则sin∠ABC=$\frac{\sqrt{5}}{5}$.