题目内容
11.解方程组(1)$\left\{\begin{array}{l}{x+y=1}\\{2x-y=-4}\end{array}\right.$
(2)$\left\{\begin{array}{l}{3(x-1)=4(y-4)}\\{5(y-1)=3(x+5)}\end{array}\right.$.
分析 (1)利用加减消元法消去y,比较简单.
(2)先把组中的方程化简后,再求方程组的解.
解答 解:(1)$\left\{\begin{array}{l}{x+y=1①}\\{2x-y=-4②}\end{array}\right.$
①+②,得3x=-3,
所以x=-1
把x=-1代入①,得y=2
所以原方程组的解为$\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$
(2)原方程化简得$\left\{\begin{array}{l}{3x-4y=-13①}\\{5y-3x=20②}\end{array}\right.$
①+②,得y=7,
把y=7代入①,得x=5
所以原方程组的解为$\left\{\begin{array}{l}{x=5}\\{y=7}\end{array}\right.$
点评 本题考查了二元一次方程组的解法.根据组中方程系数的特点,灵活选用代入消元或加减消元.本组中的(2)亦可变形5(y-1)=3(x+5)为5(y-1)=3(x-1)+18,然后把3(x-1)=4(y-4)整体代入求解.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
8.某种细胞的直径是0.00000089米,将0.00000089用科学记数法表示为( )
| A. | 89×10-8 | B. | 8.9×10-8 | C. | 0.89×10-7 | D. | 8.9×10-7 |
3.下列各式从左到右是分解因式的是( )
| A. | 10x3y4=2xy•5x2y3 | B. | 4a2-4ab+b2=(2a-b)2 | ||
| C. | (a-b)(a+b)=a2-b2 | D. | x2+3x-5=(x-1)(x+4)-1 |
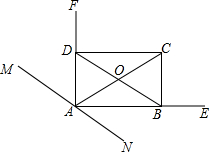 如图所示,AF是∠MAC角平分线,AE是∠NAC的角平分线,OB=OD,且OA=OC,求证:四边形ABCD为矩形.
如图所示,AF是∠MAC角平分线,AE是∠NAC的角平分线,OB=OD,且OA=OC,求证:四边形ABCD为矩形.
 已知:如图,平行四边形ABCD的对角线相交于点O,点E在边BC的延长线上,且OE=OB,联结DE.
已知:如图,平行四边形ABCD的对角线相交于点O,点E在边BC的延长线上,且OE=OB,联结DE.