题目内容
2.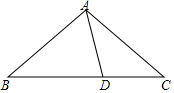 如图,在△ABC中,点D在边BC上,AC=BD,∠CAD=30°,∠ACB=40°,则∠ABC=40°.
如图,在△ABC中,点D在边BC上,AC=BD,∠CAD=30°,∠ACB=40°,则∠ABC=40°.
分析 作辅助线,构建两个三角形全等,证明△AEB≌△ADC,可以得∠ABC=∠ACB=40°.
解答 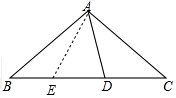 解:在BC上取一点E,使EC=AC,
解:在BC上取一点E,使EC=AC,
∴∠AEC=∠EAC,
∵∠ACB=40°,
∴∠AEC=∠EAC=$\frac{180°-40°}{2}$=70°,
∵AC=EC,BD=AC,
∴BD=EC,
∴BD-DE=EC-ED,
∴BE=DC,
∵∠DAC=30°,
∴∠ADB=∠DAC+∠ACB=30°+40°=70°,
∴∠AEC=∠ADB=70°,
∴AE=AD,∠AEB=∠ADC,
∴△AEB≌△ADC(SAS),
∴∠ABC=∠ACB=40°,
故答案为:40°.
点评 本题考查了全等三角形、等腰三角形的性质和判定、外角定理,辅助线的作出是本题的关键,∠AEC和∠ADB相等的证明是本题的突破口,利用等腰三角形等角对等边和等角的补角相等得出证明三角形全等的边和角,从而使问题得以解决.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
12.下列各组数分别是三条线段的长度,其中能围成直角三角形的是( )
| A. | 1,1,2 | B. | 1,2,3 | C. | 1,$\sqrt{2}$,$\sqrt{3}$ | D. | 2,3,4 |
10.下列各式错误的是( )
| A. | -4>-5 | B. | -(-3)=3 | C. | -|-4|=4 | D. | 16÷(-4)2=1 |
17.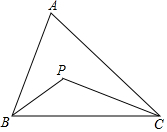 如图,在△ABC中,∠BAC=56°,∠ABC=74°,BP、CP分别平分∠ABC和∠ACB,则∠BPC=( )
如图,在△ABC中,∠BAC=56°,∠ABC=74°,BP、CP分别平分∠ABC和∠ACB,则∠BPC=( )
 如图,在△ABC中,∠BAC=56°,∠ABC=74°,BP、CP分别平分∠ABC和∠ACB,则∠BPC=( )
如图,在△ABC中,∠BAC=56°,∠ABC=74°,BP、CP分别平分∠ABC和∠ACB,则∠BPC=( )| A. | 102° | B. | 112° | C. | 115° | D. | 118° |
7.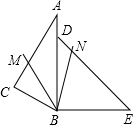 把一副三角尺ABC与BDE按如图所示那样拼在一起,其中A、D、B三点在同一直线上,BM为∠ABC的平分线,BN为∠CBE的平分线,则∠MBN的度数是( )
把一副三角尺ABC与BDE按如图所示那样拼在一起,其中A、D、B三点在同一直线上,BM为∠ABC的平分线,BN为∠CBE的平分线,则∠MBN的度数是( )
 把一副三角尺ABC与BDE按如图所示那样拼在一起,其中A、D、B三点在同一直线上,BM为∠ABC的平分线,BN为∠CBE的平分线,则∠MBN的度数是( )
把一副三角尺ABC与BDE按如图所示那样拼在一起,其中A、D、B三点在同一直线上,BM为∠ABC的平分线,BN为∠CBE的平分线,则∠MBN的度数是( )| A. | 30° | B. | 45° | C. | 55° | D. | 60° |
11.下面式子从左边到右边的变形是因式分解的是( )
| A. | x2-x-2=x(x-1)-2 | B. | (x+1)(x-1)=x2-1 | C. | x2-4x+4=(x-2)2 | D. | x-1=x(1-$\frac{1}{x}$) |
12. 如图,菱形ABCD的周长为16,∠ABC=120°,则DB的长为( )
如图,菱形ABCD的周长为16,∠ABC=120°,则DB的长为( )
 如图,菱形ABCD的周长为16,∠ABC=120°,则DB的长为( )
如图,菱形ABCD的周长为16,∠ABC=120°,则DB的长为( )| A. | $4\sqrt{3}$ | B. | 4 | C. | $2\sqrt{3}$ | D. | 2 |
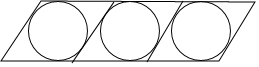 如图,花边带上菱形的内切圆半径均为1cm,若菱形有一个内角为60°,且这条花边带有50个圆和50个菱形,求这条花边上、下边长的和.
如图,花边带上菱形的内切圆半径均为1cm,若菱形有一个内角为60°,且这条花边带有50个圆和50个菱形,求这条花边上、下边长的和.