题目内容
1.在Rt△ABC中,∠C=90°,求sin2A+sin2B的值.分析 根据互余两角三角函数的关系,可得答案.
解答 解:Rt△ABC中,∠C=90°,
sin2A+sin2B=$\frac{{a}^{2}}{{c}^{2}}$+$\frac{{b}^{2}}{{c}^{2}}$=$\frac{{c}^{2}}{{c}^{2}}$=1.
点评 本题考查了互余两角三角函数的关系,互余两角三角函数的关系:sin2A+sin2B=1.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
12.一元二次方程x2-x=0的解为( )
| A. | 0 | B. | 1 | C. | 0或1 | D. | 此方程无实数解 |
6.一水池有甲乙两个进水管,两出水管,甲单独注水,20小时可注满水池,乙单独注水40小时可注满水池,单独开放水管,30小时可能放光一池水,现甲乙两管齐开8小时后,再打开两管,问还需几个小时注满一池水?
10.下列函数的图象中与一次函数y=-2x+2的图象相交于点(1,0)的是( )
| A. | y=x+1 | B. | y=x-1 | C. | y=-4x+1 | D. | y=4x+1 |
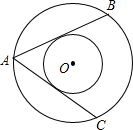 如图,在两个同心圆O中,AB、AC都是大圆的弦,且AB=AC,AB为小圆的切线,则AC与小圆相切吗?请说明理由.
如图,在两个同心圆O中,AB、AC都是大圆的弦,且AB=AC,AB为小圆的切线,则AC与小圆相切吗?请说明理由.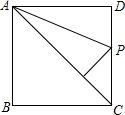 如图,正方形ABCD的边长为4cm,动点P从点D开始沿着D→C→B的路线以1cm/s的速度移动,到达点B停止运动,设点P的运动时间为x s,解答下列问题:
如图,正方形ABCD的边长为4cm,动点P从点D开始沿着D→C→B的路线以1cm/s的速度移动,到达点B停止运动,设点P的运动时间为x s,解答下列问题: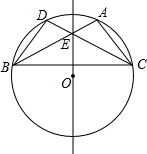 如图所示,在⊙O中,弦AB与DC相交于点E,AB=CD.
如图所示,在⊙O中,弦AB与DC相交于点E,AB=CD.