题目内容
9.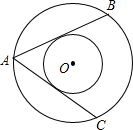 如图,在两个同心圆O中,AB、AC都是大圆的弦,且AB=AC,AB为小圆的切线,则AC与小圆相切吗?请说明理由.
如图,在两个同心圆O中,AB、AC都是大圆的弦,且AB=AC,AB为小圆的切线,则AC与小圆相切吗?请说明理由.
分析 过点O作OE⊥AC于E,只要证明OE是小圆的半径即可.设小圆与AB的切点为D,连接OD、OA,根据垂径定理以及AB=AC,可得AD=AE,从而可证△AEO与△ADO全等,故OE=OD.
解答 解:过点O作OE⊥AC于E,设小圆与AB的切点为D,连接OD、OA,如图,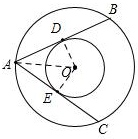
由切线性质可知OD⊥AB,
由垂径定理可知AD=DB,AE=EC,
∵AB=AC,
∴AD=AE,
在Rt△AEO和Rt△ADO中,
$\left\{\begin{array}{l}{AE=AD}\\{AO=AO}\end{array}\right.$
∴△AEO≌△ADO(HL),
∴OE=OD,
∴AC与小圆相切.
点评 本题考查了圆的切线的性质与判定,属于基础题.清楚切线的性质定理与判定定理以及垂径定理是解答的关键.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
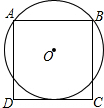 如图,⊙O过正方形ABCD的顶点A、B,且与CD相切.若正方形ABCD的边长为2,则⊙O的半径为$\frac{5}{4}$.
如图,⊙O过正方形ABCD的顶点A、B,且与CD相切.若正方形ABCD的边长为2,则⊙O的半径为$\frac{5}{4}$.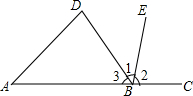 如图,
如图, 如图,将三个形状、大小完全一样的正方形的一个顶点重合放置,∠FAG=45°,∠BAC=30°,求∠DAE的度数.
如图,将三个形状、大小完全一样的正方形的一个顶点重合放置,∠FAG=45°,∠BAC=30°,求∠DAE的度数.