题目内容
13.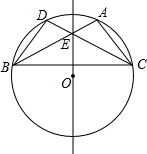 如图所示,在⊙O中,弦AB与DC相交于点E,AB=CD.
如图所示,在⊙O中,弦AB与DC相交于点E,AB=CD.(1)求证:△AEC≌△DEB;
(2)连接BC,判断直线OE与BC的位置关系,并说明理由.
分析 (1)要证△AEC≌△DEB,由于AB=CD,根据等弦所对的弧相等得$\widehat{AB}$=$\widehat{CD}$,根据等量减等量还是等量,得$\widehat{BD}$=$\widehat{CA}$,由等弧对等弦得BD=CA,由圆周角定理得,∠ACE=∠DBE,∠AEC=∠DEB,即可根据AAS判定;
(2)由△AEC≌△DEB得,BE=CE,得到点E在直线BC的中垂线上,连接BO,CO,BO和CO是半径,则BO和CO相等,即点O在线段BC的中垂线上,亦即直线EO是线段BC的中垂线,OE⊥BC.
解答  (1)证明:∵AB=CD,
(1)证明:∵AB=CD,
∴$\widehat{AB}$=$\widehat{CD}$.
∴$\widehat{AB}$-$\widehat{AD}$=$\widehat{CD}$-$\widehat{AD}$.
∴$\widehat{BD}$=$\widehat{CA}$.
∴BD=CA.
在△AEC与△DEB中,
$\left\{\begin{array}{l}{∠ACE=∠DBE}\\{∠AEC=∠DEB}\\{BD=CA}\end{array}\right.$,
∴△AEC≌△DEB(AAS).
(2)解:OE⊥BC,
如图,连接OB、OC、BC.
由(1)得BE=CE.
∴点E在线段BC的中垂线上,
∵BO=CO,
∴点O在线段BC的中垂线上,
∴OE⊥BC.
点评 本题考查了圆周角定理、等弦所对的弧相等,等弧对等弦、全等三角形的判定和性质,熟练掌握性质定理是解题的关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
2.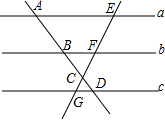 如图,a∥b∥c,AB=3,BC=2,CD=1,那么下列式子中不成立的是( )
如图,a∥b∥c,AB=3,BC=2,CD=1,那么下列式子中不成立的是( )
 如图,a∥b∥c,AB=3,BC=2,CD=1,那么下列式子中不成立的是( )
如图,a∥b∥c,AB=3,BC=2,CD=1,那么下列式子中不成立的是( )| A. | EC:CG=5:1 | B. | EF:FC=1:1 | C. | EF:FC=3:2 | D. | EF:EC=3:5 |
 如图,
如图,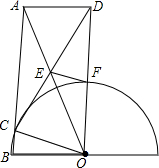 如图.在△AB0中,AB=A0=2B0,以O为圆心,OB为半径的半圆交AB边于点C.△ABO绕点O顺时针旋转得△DCO,DC交AO于点E,DO交半圆于点F,连接AD,EF.
如图.在△AB0中,AB=A0=2B0,以O为圆心,OB为半径的半圆交AB边于点C.△ABO绕点O顺时针旋转得△DCO,DC交AO于点E,DO交半圆于点F,连接AD,EF. 设甲、乙两车在同一直线公路上匀速行驶,开始甲车在乙车的前面,当乙车追上甲车后,两车停下来,把乙车的货物转给甲车,然后甲车继续前行,乙车向原地返回,设x秒后两车间的距离为y千米,y关于x的函数关系如图所示.
设甲、乙两车在同一直线公路上匀速行驶,开始甲车在乙车的前面,当乙车追上甲车后,两车停下来,把乙车的货物转给甲车,然后甲车继续前行,乙车向原地返回,设x秒后两车间的距离为y千米,y关于x的函数关系如图所示.