题目内容
将一副三角板按如图1位置摆放,使得两块三角板的直角边AC和MD重合.已知AB=AC=8cm,将△MED绕点A(M)逆时针旋转60°后(图2),两个三角形重叠(阴影)部分的面积是 cm2.
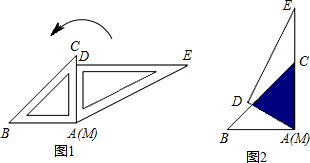
考点:旋转的性质
专题:
分析:设MD与BC交于F,过F作FH⊥AC于H,如图2,先根据旋转的性质得∠FAC=60°,在△FHC中,由于∠FCH=45°,则CH=FH,设CH=x,则FH=x,
在Rt△FHA中,由于∠FAH=60°,则AH=
FH=
x,然后利用CH+AH=AC得到x+
x=8,解得x=4(3-
),再根据三角形面积公式计算得到S△FAC=
FH•AC=(48-16
)cm2.
在Rt△FHA中,由于∠FAH=60°,则AH=
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| 3 |
| 1 |
| 2 |
| 3 |
解答: 解:设MD与BC交于F,过F作FH⊥AC于H,如图2,
解:设MD与BC交于F,过F作FH⊥AC于H,如图2,
∠ACB=45°,∠DME=60°,AC=8cm,
∵△MED绕点A(M)逆时针旋转60°后得到图2,
∴∠FAC=60°,
在△FHC中,∠FCH=45°,
∴CH=FH,
设CH=x,则FH=x,
在Rt△FHA中,∠FAH=60°,
∴AH=
FH=
x,
∵CH+AH=AC,
∴x+
x=8,解得x=4(3-
),
∴S△FAC=
FH•AC=
×4(3-
)×8=(48-16
)cm2.
故答案为(48-16
).
 解:设MD与BC交于F,过F作FH⊥AC于H,如图2,
解:设MD与BC交于F,过F作FH⊥AC于H,如图2,∠ACB=45°,∠DME=60°,AC=8cm,
∵△MED绕点A(M)逆时针旋转60°后得到图2,
∴∠FAC=60°,
在△FHC中,∠FCH=45°,
∴CH=FH,
设CH=x,则FH=x,
在Rt△FHA中,∠FAH=60°,
∴AH=
| ||
| 3 |
| ||
| 3 |
∵CH+AH=AC,
∴x+
| ||
| 3 |
| 3 |
∴S△FAC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
故答案为(48-16
| 3 |
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
点(6,-8)是直角坐标系中的一点,O为坐标原点,则OA的长度为( )
| A、6 | B、8 | C、10 | D、12 |
下列计算正确的是( )
| A、(a5)2=a7 |
| B、b3•b3=2b3 |
| C、a3÷a=a3 |
| D、a3•a2=a5 |
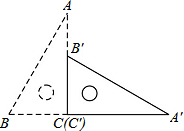 如图,直角三角板ABC的斜边AB=12cm,∠A=30°,将三角板ABC绕C顺时针旋转90°至三角板A′B′C′的位置后,再沿CB方向向左平移,使点B′落在原三角板ABC的斜边AB上,则三角板A′B′C′平移的距离为
如图,直角三角板ABC的斜边AB=12cm,∠A=30°,将三角板ABC绕C顺时针旋转90°至三角板A′B′C′的位置后,再沿CB方向向左平移,使点B′落在原三角板ABC的斜边AB上,则三角板A′B′C′平移的距离为 如图,每个小正方形边长为1,则△ABC边AC上的高BD的长为
如图,每个小正方形边长为1,则△ABC边AC上的高BD的长为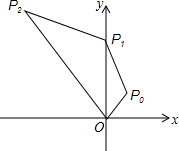 如图,在直角坐标系中,点P0的坐标为(
如图,在直角坐标系中,点P0的坐标为(