题目内容

如图为菱形ABCD与△ABE的重叠情形，其中D在BE上．若AB=17，BD=16，AE=25，则DE的长度
 
．
考点：菱形的性质
专题：
分析：作AF⊥BD于F，由等腰三角形的性质及勾股定理就可以求出AF的值，在Rt△AFE中由勾股定理就可以求出EF的值，进而就可以求出DE的值．
解答：解：作AF⊥BD于F．
∵四边形ABCD是菱形，
∴AB=AD．
∵AF⊥BD，
∴BF=DF=
1
2
BD．
∵BD=16，
∴DF=8．
在Rt△AFD中，由勾股定理，得
AF=15．
在Rt△AFE中，由勾股定理，得
EF=20．
∴DE=20-8=12．
故答案为：12．
点评：本题考查了菱形的性质的运用，等腰三角形的判定及性质的运用，勾股定理的运用，解答时运用勾股定理求解是关键．
练习册系列答案
相关题目
“数学是一种知识，更是一种过程．”同学们回忆一下，我们在研究数学知识时经常会经历这样的过程：根据给定的研究对象，构造（或研究）对象的特殊情况，再通过猜想、推理提炼对象的一般情况，最后对研究对象验证和实践的思维活动过程．
例如：比较nr+1和（n+1）r的大小（n≥1的整数），我们可以从分析n=1，n=2，n=3，…，这些简单情形入手，从中发现规律，经过归纳，猜想出结论．进而应用归纳出的结论比较两个数20102013和20112014等数的大小．
在研究真分数
a
b
（a、b均为正数）和真分数
a+m
b+m
（m为正数）的大小时，我们可以用上面的思想和方法进行研究：
研究特殊情况：
（1）任意写一些正的真分数
1
2
、
 
、
 
…，给每个分数的分子和分母同加一个正数得到新分数：
1+1
2+1
、
 
、
 
…
提炼一般情况：
（2）比较原来每个分数与对应新分数的大小，可以得出下面的结论：一个真分数是
a
b
（a、b均为正数），给其分子分母同加一个正数m，得
a+m
b+m
，则两个分数的大小关系是
a+m
b+m
 
a
b
．
解决问题：
（3）利用上述原理简要说明一杯糖水加上一勺糖更甜的理由．
 
．
如图，P是正方形ABCD内任意一点，△APD与△BPC的面积之和为8cm2，则AB=
 
cm．
若m-n=-1，则m2-n2+m+n=
 
．
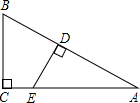在Rt△ABC中，∠C=90°，∠A=30°，点D，E分别在AB，AC上，若DE将△ABC分成面积相等的两部分，且△ABC的面积为20，AE=8，则AD=
 
．
已知二次函数y=kx2-7x-7的图象与x轴有两个交点，则k的取值范围为
 
．
一副扑克牌52张（不含鬼牌），分为黑桃、红心、方块及梅花4种花色，每种花色各有13张，分别标有字母A、K、Q、J和数字10、9、8、7、6、5、4、3、2．从这副牌中任意抽出一张，则这张牌是标有字母的牌的概率是
 
．
如图，用含a、b、c的代数式表示图中阴影部分的面积为
 
．
下列四个命题中说法正确是（　　）
①对顶角相等； ②两点之间线段最短； ③同位角相等； ④半圆所对的圆周角是直角．
A、①②③B、①②④
C、②③④D、①③④

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网