题目内容
19．在△ABC中，∠C=90°，AC=3，AB=$\sqrt{14}$．求sinA，cosA，sinB，cosB的值．分析 先运用勾股定理求得BC的长度，然后根据三角函数的定义求解即可．
解答 解：在△ABC中，
∵∠C=90°，AC=3，AB=$\sqrt{14}$，
∴BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=$\sqrt{5}$，
∴sinA=$\frac{BC}{AB}=\frac{\sqrt{5}}{\sqrt{14}}$=$\frac{\sqrt{70}}{14}$，cosA=$\frac{AC}{AB}=\frac{3}{\sqrt{14}}$=$\frac{3\sqrt{14}}{14}$，sinB=$\frac{AC}{AB}$=$\frac{3\sqrt{14}}{14}$，cosB=$\frac{BC}{AB}$=$\frac{\sqrt{70}}{14}$．
点评 本题考查了锐角三角函数的定义以及勾股定理，属于基础题，掌握三角函数的定义是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
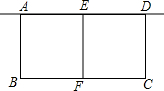如图是一个矩形养鸡场的平面图，养鸡场由一堵旧墙（旧墙的长度不小于l米）和总长为l0米的篱笆围成，中间用篱笆分隔成两个小矩形．设大矩形的垂直于旧墙的一边长为x米，面积为s平方米．求s关于x的函数解析式，并写出这个函数的定义域．
如图，在Rt△ABC中，CD是斜边AB上的高，S△ABC=4，AC=4．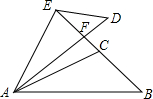
如图所示，△ABC≌△ADE，BC的延长线过点E，∠ACB=∠AED=105°，∠CAD=10°，∠B=50°，∠DEF的度数是35°．
如图，A，B两点的坐标分别是A（1，2），B（2，0），则△ABO的面积是2．