题目内容
2.抛物线y=-(-x-8)2+2的顶点所在象限是( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 根据抛物线的顶点式求出顶点坐标,再根据各象限内点的坐标特点进行解答.
解答 解:抛物线y=-(-x-8)2+2的顶点坐标为(-8,2),
所以顶点在第二象限.
故选:B.
点评 本题考查的是二次函数的性质及各象限内点的坐标特点,根据题意得出抛物线的顶点坐标是解答此题的关键.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
12.计算(2-5)+(-1)的结果是( )
| A. | 2 | B. | -2 | C. | 4 | D. | -4 |
10.下列各等式中,成立的是( )
| A. | -a+b=-(a+b) | B. | 3x+8=3(x+8) | C. | 2-5x=-(5x-2) | D. | 12x-4=8x |
14.用配方法解一元二次方程x2+4x+3=0,下列配方正确的是( )
| A. | (x+2)2=1 | B. | (x-2)2=1 | C. | (x+2)2=7 | D. | (x-2)2=7 |
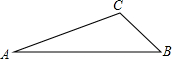 已知:如图,△ABC中,AC=12cm,AB=12$\sqrt{2}$cm,sinA=$\frac{1}{3}$
已知:如图,△ABC中,AC=12cm,AB=12$\sqrt{2}$cm,sinA=$\frac{1}{3}$