题目内容
1.已知a为有理数,化简:$\sqrt{-{a}^{3}}$-a$\sqrt{-\frac{1}{a}}$.分析 根据$\sqrt{{a}^{2}}$=$\left\{\begin{array}{l}{a(a≥0)}\\{-a(a<0)}\end{array}\right.$,进行化简即可.
解答 解:原式=-a$\sqrt{-a}$+$\sqrt{-a}$
=(-a+1)$\sqrt{-a}$.
点评 本题考查了二次根式的化简求值,解答此题,要弄清以下问题:
①定义:一般地,形如$\sqrt{a}$(a≥0)的代数式叫做二次根式.当a>0时,$\sqrt{a}$表示a的算术平方根;当a=0时,$\sqrt{0}$=0;当a<0时,非二次根式(在一元二次方程中,若根号下为负数,则无实数根).
②性质:$\sqrt{{a}^{2}}$=|a|.

练习册系列答案
相关题目
10.菱形的一个内角是120°,一条较短的对角线的长为10,则菱形的周长是( )
| A. | 10 | B. | 20 | C. | 30 | D. | 40 |
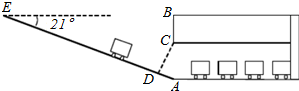 某校九年级数学兴趣小组为了测得该校地下停车场的限高CD,在课外活动时间测得下列数据:如图,从地面E点测得地下停车场的俯角为21°,斜坡AE的长为20米,地面B点(与E点在同一个水平线)距停车场顶部C点(A、C、B在同一条直线上且与水平线垂直)1.6米.试求该校地下停车场的高度AC及限高CD(结果精确到0.1米).(参考数据:sin21°≈0.28,cos21°≈0.91,tan21°≈0.43)
某校九年级数学兴趣小组为了测得该校地下停车场的限高CD,在课外活动时间测得下列数据:如图,从地面E点测得地下停车场的俯角为21°,斜坡AE的长为20米,地面B点(与E点在同一个水平线)距停车场顶部C点(A、C、B在同一条直线上且与水平线垂直)1.6米.试求该校地下停车场的高度AC及限高CD(结果精确到0.1米).(参考数据:sin21°≈0.28,cos21°≈0.91,tan21°≈0.43)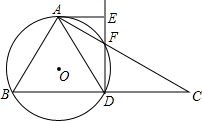 如图,在Rt△ABC中,斜边BC=12,∠C=30°,D为BC的中点,△ABD的外接圆⊙O与AC交于F点,过A作⊙O的切线AE交DF的延长线于E点.
如图,在Rt△ABC中,斜边BC=12,∠C=30°,D为BC的中点,△ABD的外接圆⊙O与AC交于F点,过A作⊙O的切线AE交DF的延长线于E点.