题目内容
4.用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成,硬纸板以如图两种方法裁剪(裁剪后边角料不再利用)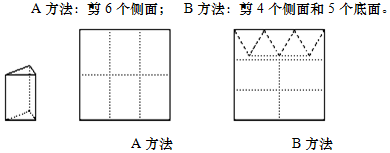
现有38张硬纸板,裁剪时x张用A方法,其余用B方法.
(1)用x的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
分析 (1)由x张用A方法,就有(38-x)张用B方法,就可以分别表示出侧面个数和底面个数;
(2)根据裁剪出的侧面和底面恰好全部用完得出方程,解方程求出x的值,求出侧面的总数就可以求出结论.
解答 解:(1)侧面个数:6x+4(38-x)=(2x+152)个.
底面个数:5(38-x)=(190-5x)个.
(2)由题意,得$\frac{2x+152}{3}$=$\frac{190-5x}{2}$.
解得:x=14.
$\frac{2x+152}{3}$=60(个).
答:若裁剪出的侧面和底面恰好全部用完,能做60个盒子.
点评 本题考查了列一元一次方程解实际问题的运用,一元一次方程的解法的运用,列代数式的运用,解答时根据裁剪出的侧面和底面个数相等建立方程是关键.

练习册系列答案
相关题目
16.己知反比例函数y=-$\frac{1}{x}$,下列结论正确的是( )
| A. | y值随着x值的增大而减小 | B. | 图象是双曲线,是中心对称图形 | ||
| C. | 当x>l时,0<y<l | D. | 图象可能与坐标轴相交 |
13. 王楠同学在如图所示的作业本上写了五个整式,其中属于同类项的是( )
王楠同学在如图所示的作业本上写了五个整式,其中属于同类项的是( )
 王楠同学在如图所示的作业本上写了五个整式,其中属于同类项的是( )
王楠同学在如图所示的作业本上写了五个整式,其中属于同类项的是( )| A. | ①和② | B. | ②和③ | C. | ①和④ | D. | ③和⑤ |
14. 如图,AB是⊙O的弦,BC与⊙O相切于点B,连接OA,OB,若∠ABC=65°,则∠A等于( )
如图,AB是⊙O的弦,BC与⊙O相切于点B,连接OA,OB,若∠ABC=65°,则∠A等于( )
 如图,AB是⊙O的弦,BC与⊙O相切于点B,连接OA,OB,若∠ABC=65°,则∠A等于( )
如图,AB是⊙O的弦,BC与⊙O相切于点B,连接OA,OB,若∠ABC=65°,则∠A等于( )| A. | 20° | B. | 25° | C. | 35° | D. | 75° |


 如图,一只蚂蚁从长、宽都是2,高是5的长方体纸盒的A点沿纸盒面爬到B点,那么它所行的最短路线的长是$\sqrt{41}$.
如图,一只蚂蚁从长、宽都是2,高是5的长方体纸盒的A点沿纸盒面爬到B点,那么它所行的最短路线的长是$\sqrt{41}$.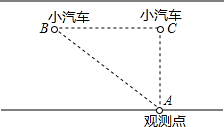 “中华人民共和国道路交通管理条例”规定:小汽车在沿海高速路上的行驶速度不能低于60千米/小时不得超过120千米/小时,如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到观测点A正前方60米处,过了3秒后,测得小汽车与观测点间的距离变为100米.这辆小汽车行驶速速度符合规定吗?(在横线上填序号①符合 ②不符合)①.
“中华人民共和国道路交通管理条例”规定:小汽车在沿海高速路上的行驶速度不能低于60千米/小时不得超过120千米/小时,如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到观测点A正前方60米处,过了3秒后,测得小汽车与观测点间的距离变为100米.这辆小汽车行驶速速度符合规定吗?(在横线上填序号①符合 ②不符合)①.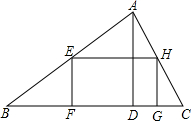 如图,在△ABC中,AD是BC上的高,且BC=9,AD=3,矩形EFGH的顶点F、G在边BC上,顶点E、H分别在边AB和AC上,如果设边EF的长为x(0<x<3),矩形EFGH的面积为y,那么y关于x的函数解析式是y=-3x2+9x(0<x<3).
如图,在△ABC中,AD是BC上的高,且BC=9,AD=3,矩形EFGH的顶点F、G在边BC上,顶点E、H分别在边AB和AC上,如果设边EF的长为x(0<x<3),矩形EFGH的面积为y,那么y关于x的函数解析式是y=-3x2+9x(0<x<3).