题目内容

14．如图，AB是⊙O的弦，BC与⊙O相切于点B，连接OA，OB，若∠ABC=65°，则∠A等于（　　）
A．20°B．25°C．35°D．75°

分析 先根据切线的性质得∠OBC=90°，则利用互余得到∠OBA=25°，然后根据等腰三角形的性质求出∠A的度数．

解答 解：∵BC与⊙O相切于点B，
∴OB⊥BC，
∴∠OBC=90°，
∴∠OBA=90°-∠ABC=90°-65°=25°，
而OA=OB，
∴∠A=∠OBA=25°．
故选B．

点评 本题考查了切线的性质：圆的切线垂直于经过切点的半径．若出现圆的切线，必连过切点的半径，构造定理图，得出垂直关系．

练习册系列答案
相关题目
4．用正方形硬纸板做三棱柱盒子，每个盒子由3个矩形侧面和2个正三角形底面组成，硬纸板以如图两种方法裁剪（裁剪后边角料不再利用）

现有38张硬纸板，裁剪时x张用A方法，其余用B方法．
（1）用x的代数式分别表示裁剪出的侧面和底面的个数；
（2）若裁剪出的侧面和底面恰好全部用完，问能做多少个盒子？
5．二次函数y=ax2+bx+c（a≠0）的图象如图所示，下列说法：①a＞0；②b＞0；③c＜0；b2-4ac＞0中，正确的个数有（　　）
A．1B．2C．3D．4
2．一个整式减去a-b后所得的结果是-a-b，这这个整式是（　　）
A．-2aB．-2bC．2aD．2b
9．已知P1（x1，y1），P2（x2，y2），P3（x3，y3）是反比例函数y=$\frac{2}{x}$的图象上的三点，且x1＜x2＜0＜x3，则y1、y2、y3的大小关系是 （　　）
A．y3＜y2＜y1B．y2＜y1＜y3C．y1＜y2＜y3D．y2＜y3＜y1
19．下列计算正确的是（　　）
A．（a4）3=a7B．a6÷a3=a2C．（2a）3=6a3D．a•a3=a4
6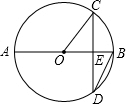．如图，AB是⊙O的直径，弦CD⊥AB，垂足为点E，连接OC，DB，若∠CDB=30°，⊙O的半径为4$\sqrt{3}$cm，则弦CD的长为（　　）
A．8$\sqrt{3}$cmB．12cmC．6$\sqrt{3}$cmD．8cm
3．下列计算中，正确的是（　　）
A．（2a）3=2a3B．a3+a2=a5C．（a2）3=a6D．a8÷a4=a2
4．某车间有26名工人，每人每天可以生产800个螺钉或1000个螺母，1个螺钉需要配2个螺母，为使每天生产的螺钉和螺母刚好配套，设安排x名工人生产螺钉，则下面所列方程正确的是（　　）
A．1000（26-x）=800xB．1000（13-x）=800xC．1000（26-x）=2×800xD．2×1000（26-x）=800x

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网