Question

6．如图，E为正方形ABCD外一点，AE=DE=3，∠AED=45°，则BE的长为3$\sqrt{3}$．

Answer 1

分析 过点E作EF⊥BC于F，交AD于G，作AE的垂直平分线交EF于点O，则点O是△ADE的外心，DG=a，则OE=OD=$\sqrt{2}$a，FG=2a，BF=a，在Rt△DEG中，利用勾股定理求出a²，再在Rt△EFB中，利用勾股定理求出BE即可．

解答 解：过点E作EF⊥BC于F，交AD于G，作AE的垂直平分线交EF于点O，则点O是△ADE的外心，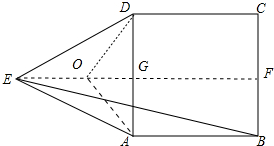

∴∠AOD=2∠DEA=90°，OA=OD=OE，
∴OG=DG=AG，设DG=a，则OE=OD=$\sqrt{2}$a，FG=2a，BF=a，
在Rt△DEG中，DE²=EG²+DG²，
∴9=（a+$\sqrt{2}$a）²+a²，解得a²=$\frac{9}{2（2+\sqrt{2}）}$，
∴BE=$\sqrt{B{F}^{2}+E{F}^{2}}$=$\sqrt{{a}^{2}+（3a+\sqrt{2}a）^{2}}$=$\sqrt{6（2+\sqrt{2}）{a}^{2}}$=3$\sqrt{3}$．
故答案为3$\sqrt{3}$．

点评 本题考查正方形的性质、勾股定理，三角形的外心等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题，属于中考常考题型．