题目内容
16.已知数轴上两点A、B对应的数分别为a和b,且满足|a+4|+(b-3)2=0,点M为数轴上一动点,请回答下列问题:(1)请直接写出a、b的值,并画出图形;
(2)点M为数轴上一动点,点A、B不动,问线段BM与AM的差即BM-AM的值是否一定发生变化?请回答.
(3)设点A以每秒x个单位向左运动,点M从表示y数的点以每秒x个单位向左运动,点B以每秒y个单位向右运动t秒后
①A、B、M三点分别表示什么数(用x、y、t表示);
②线段BM与AM的差即BM-AM的值是否一定发生变化?请回答,并说明理由.
分析 (1)由绝对值的非负性得:a+4=0,由偶次方的非负性得:b-3=0,解出并画数轴;
(2)先根据数轴上两点的距离表示出BM和AM的长,再分三种情况进行讨论::①当点M在点B的右侧,②当点M在点A与B之间时,③当点M在点A的左侧时;代入计算即可;
(3)①分别表示出A、B、M三点表示的数,向左减,向右加;
②同理按(2)分三种情况计算.
解答 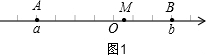 解:(1)如图1,由题意得:a+4=0,b-3=0,
解:(1)如图1,由题意得:a+4=0,b-3=0,
则a=-4,b=3;
(2)线段BM与AM的差即BM-AM的值发生变化,理由是:
设点M对应的数为c,
由BM=|c-b|,AM=|c-a|,
则分三种情况:①当点M在点B的右侧时,如图2,BM-AM=c-b-c+a=a-b=-4-3=-7,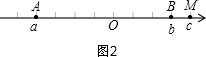
②当点M在点A与B之间时,BM-AM=b-c-c+a=a+b-2c=-4+3-2c=-1-2c,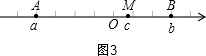
③当点M在点A的左侧时,BM-AM=b-c-a+c=b-a=3+4=7,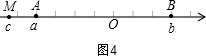
(3)①点A表示的数为:-4-tx;点B表示的数为:3+yt;点M表示的数为:y-tx;
②线段BM与AM的差即BM-AM的值一定发生变化,理由是:
分三种情况:
i)当点M在点B的右侧时,如图2,BM-AM=-AB=-(3+yt+4+tx)=-7-yt-tx,
ii)当点M在点A与B之间时,如图3,BM-AM=3+yt-y+tx-(y-tx+4+tx)=-1-2y+tx+yt,
iii)当点M在点A的左侧时,BM-AM=AB=3+yt+4+tx=7+yt+tx.
点评 本题考查了数轴及绝对值与偶次方的非负性,掌握数轴上两点的距离公式:若点A表示a,点B表示b时,AB=|xb-xa|,同时如果出现几个非负数的和为零时,则令每个非负数为零,列方程计算即可.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
11. 我校为了迎接体育中考,了解学生的体育成绩,从全校1000名九年级学生中随机抽取了部分学生进行体育测试,其中“跳绳”成绩制作图如下:
我校为了迎接体育中考,了解学生的体育成绩,从全校1000名九年级学生中随机抽取了部分学生进行体育测试,其中“跳绳”成绩制作图如下:
根据图表解决下列问题:
(1)本次共抽取了50名学生进行体育测试,表(1)中,a=0.2,b=7c=0.32;
(2)补全图(2);
(3)“跳绳”数在180(包括180)以上,则此项成绩可得满分.那么,你估计全校九年级有多少学生在此项成绩中获满分?
 我校为了迎接体育中考,了解学生的体育成绩,从全校1000名九年级学生中随机抽取了部分学生进行体育测试,其中“跳绳”成绩制作图如下:
我校为了迎接体育中考,了解学生的体育成绩,从全校1000名九年级学生中随机抽取了部分学生进行体育测试,其中“跳绳”成绩制作图如下:| 成绩段 | 频数 | 频率 |
| 160≤x<170 | 5 | 0.1 |
| 170≤x<180 | 10 | a |
| 180≤x<190 | b | 0.14 |
| 190≤x<200 | 16 | c |
| 200≤x<210 | 12 | 0.24 |
(1)本次共抽取了50名学生进行体育测试,表(1)中,a=0.2,b=7c=0.32;
(2)补全图(2);
(3)“跳绳”数在180(包括180)以上,则此项成绩可得满分.那么,你估计全校九年级有多少学生在此项成绩中获满分?
 如图,E为正方形ABCD外一点,AE=DE=3,∠AED=45°,则BE的长为3$\sqrt{3}$.
如图,E为正方形ABCD外一点,AE=DE=3,∠AED=45°,则BE的长为3$\sqrt{3}$. 如图,在△ABC中,AB=AC,D在AB上,E在AC的延长线上,DE交BC于F,且CE=BD,求证:DE>BC.
如图,在△ABC中,AB=AC,D在AB上,E在AC的延长线上,DE交BC于F,且CE=BD,求证:DE>BC. 如图,△ABC中,AB=6,AC=4,AD是∠BAC的外角平分线,CD⊥AD于D,且点E是BC的中点,则DE=5.
如图,△ABC中,AB=6,AC=4,AD是∠BAC的外角平分线,CD⊥AD于D,且点E是BC的中点,则DE=5.

 如图,矩形ABCD的对角线AC与BD相交于点M,矩形MNPQ与矩形ABCD全等,射线MN与MQ分别交BC边于E、F两点,若AB=2,求证:$\frac{1}{M{E}^{2}}$+$\frac{1}{M{F}^{2}}$=1.
如图,矩形ABCD的对角线AC与BD相交于点M,矩形MNPQ与矩形ABCD全等,射线MN与MQ分别交BC边于E、F两点,若AB=2,求证:$\frac{1}{M{E}^{2}}$+$\frac{1}{M{F}^{2}}$=1.