Question

15．在Rt△ABC中，∠ACB=90°，CD是斜边AB上的中线，过点A作AE⊥CD，AE分别与中线CD，边CB相交于点H，E，AH=2CH，请画出示意图并求出sinB的值．

Answer 1

分析 根据∠ACB=90°，CD是斜边AB上的中线，可得出CD=BD，则∠B=∠BCD，再由AE⊥CD，可证明∠B=∠CAH，由AH=2CH，可得出CH：AC=1：$\sqrt{5}$，即可得出sinB的值；

解答 解：根据题意画出图形如图所示，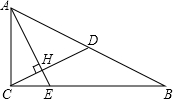

∵∠ACB=90°，CD是斜边AB上的中线，
∴CD=BD，
∴∠B=∠BCD，
∵AE⊥CD，
∴∠CAH+∠ACH=90°，
又∠ACB=90°
∴∠BCD+∠ACH=90°
∴∠B=∠BCD=∠CAH，即∠B=∠CAH，
∵AH=2CH，
∴由勾股定理得AC=$\sqrt{5}$CH，
∴CH：AC=1：$\sqrt{5}$，
∴sinB=$\frac{\sqrt{5}}{5}$．

点评 此题是解直角三角形，主要考查了解直角三角形以及直角三角形斜边上的中线，垂线，锐角三角函数，注意性质的应用，难度不大．