题目内容
15. 如图,AB∥CD∥EF,若∠A=30°,∠AFC=15°,则∠C=15°.
如图,AB∥CD∥EF,若∠A=30°,∠AFC=15°,则∠C=15°.
分析 根据平行线的性质得到∠A=∠AFE=30°,由角的和差得到∠CFE=∠AFE-∠AFC=15°,根据平行线的性质即可得到结论.
解答 解:∵AB∥CD,
∴∠A=∠AFE=30°,
∴∠CFE=∠AFE-∠AFC=15°,
∵CD∥EF,
∴∠C=∠CFE=15°,
故答案为:15°.
点评 本题考查了平行线的性质:两直线平行,同位角相等.熟记平行线的性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.如图,直角边长为1的等腰直角三角形与边长为2的正方形在同一水平线上,三角形沿水平线从左向右匀速穿过正方形.设穿过时间为t,正方形与三角形不重合部分的面积为s(阴影部分),则s与t的大致图象为( )


| A. | 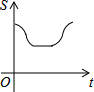 | B. | 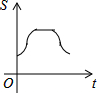 | C. | 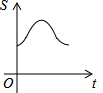 | D. |  |
3.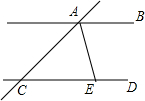 如图,直线AB∥CD,AE平分∠CAB.AE与CD相交于点E,∠ACD=40°,则∠BAE的度数是( )
如图,直线AB∥CD,AE平分∠CAB.AE与CD相交于点E,∠ACD=40°,则∠BAE的度数是( )
 如图,直线AB∥CD,AE平分∠CAB.AE与CD相交于点E,∠ACD=40°,则∠BAE的度数是( )
如图,直线AB∥CD,AE平分∠CAB.AE与CD相交于点E,∠ACD=40°,则∠BAE的度数是( )| A. | 40° | B. | 70° | C. | 80° | D. | 140° |
10.函数y=$\frac{1}{\sqrt{2x-1}}$自变量x的取值范围是( )
| A. | x≤$\frac{1}{2}$ | B. | x≥$\frac{1}{2}$ | C. | x$<\frac{1}{2}$ | D. | x>$\frac{1}{2}$ |
7.计算(-a3)2结果正确的是( )
| A. | a5 | B. | -a5 | C. | -a6 | D. | a6 |
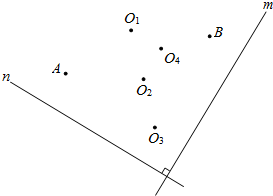 如图,直线m⊥n,在某平面直角坐标系中,x轴∥m,y轴∥n,点A的坐标为(-4,2),点B的坐标为(2,-4),则坐标原点为( )
如图,直线m⊥n,在某平面直角坐标系中,x轴∥m,y轴∥n,点A的坐标为(-4,2),点B的坐标为(2,-4),则坐标原点为( )