题目内容
3. 请你在如图所示的12×12的网格图形中,到A点的距离为5的格点的个数是( )
请你在如图所示的12×12的网格图形中,到A点的距离为5的格点的个数是( )| A. | 4 | B. | 8 | C. | 12 | D. | 16 |
分析 由$\sqrt{{3}^{2}+{4}^{2}}$=5,得出以A为圆心,5为半径的圆与网格的交点为格点的共有12个即可.
解答 解:如图所示:
∵$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴到A点的距离为5的格点的个数是12个;
故选:C.
点评 本题考查了勾股定理、圆的知识;由勾股定理和已知条件得出以A为圆心,5为半径的圆与网格的交点为格点的个数是解决问题的关键.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
13.已知a+13=b+9=c+3,则a2+b2+c2-ab-cb-ac=( )
| A. | 259 | B. | 179.5 | C. | 76 | D. | 152 |
18.已知点A表示的数为2,则到A点的距离为3表示的数为多少?( )
| A. | -1 | B. | 5 | C. | 3 | D. | -1或5 |
12.若△ABC∽△DEF,且面积比为1:3,则△ABC与△DEF的周长比为( )
| A. | 1:3 | B. | 1:9 | C. | 1:$\sqrt{3}$ | D. | 3:1 |
13.若x=2是方程2a-3x=6的解,则a的值是( )
| A. | $\frac{1}{2}$ | B. | -4 | C. | $\frac{2}{3}$ | D. | 6 |
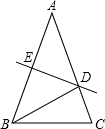 如图,△ABC中,AB=AC=5,AB的垂直平分线DE交AB、AC于E、D.
如图,△ABC中,AB=AC=5,AB的垂直平分线DE交AB、AC于E、D.