题目内容
8.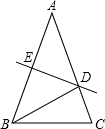 如图,△ABC中,AB=AC=5,AB的垂直平分线DE交AB、AC于E、D.
如图,△ABC中,AB=AC=5,AB的垂直平分线DE交AB、AC于E、D.(1)若△BCD的周长为8,求BC的长;
(2)若∠A=40°,求∠DBC的度数.
分析 (1)根据线段垂直平分线定理得出AD=BD,根据BC+CD+BD=8cm求出AC+BC=8cm,把AC的长代入求出即可;
(2)已知∠A=40°,AB=AC可得∠ABC=∠ACB,再由线段垂直平分线的性质可求出∠ABC=∠A,易求∠DBC.
解答 解:(1)∵D在AB垂直平分线上,
∴AD=BD,
∵△BCD的周长为8cm,
∴BC+CD+BD=8cm,
∴AD+DC+BC=8cm,
∴AC+BC=8cm,
∵AB=AC=5cm,
∴BC=8cm-5cm=3cm;
(2)∵∠A=40°,AB=AC,
∴∠ABC=∠ACB=70°,
又∵DE垂直平分AB,
∴DB=AD
∴∠ABD=∠A=40°,
∴∠DBC=∠ABC-∠ABD=70°-40°=30°.
点评 本题考查了等腰三角形性质和线段垂直平分线定理,关键是求出AC+BC的值,注意:线段垂直平分线上的点到线段的两端点的距离相等.

练习册系列答案
相关题目
19.把方程$\frac{1}{2}x=1$变形为x=2,其依据是( )
| A. | 等式的两边同时乘以$\frac{1}{2}$ | B. | 等式的两边同时除以$\frac{1}{2}$ | ||
| C. | 等式的两边同时减去$\frac{1}{2}$ | D. | 等式的两边同时加上$\frac{1}{2}$ |
3. 请你在如图所示的12×12的网格图形中,到A点的距离为5的格点的个数是( )
请你在如图所示的12×12的网格图形中,到A点的距离为5的格点的个数是( )
 请你在如图所示的12×12的网格图形中,到A点的距离为5的格点的个数是( )
请你在如图所示的12×12的网格图形中,到A点的距离为5的格点的个数是( )| A. | 4 | B. | 8 | C. | 12 | D. | 16 |
13.某超市有一种商品,进价为2元,据市场调查,销售单价是13元时,平均每天销售量是50件,而销售价每降低1元,平均每天就可以多售出10件.若设降价后售价为x元,每天利润为y元,则y与x之间的函数关系为( )
| A. | y=10x2-100x-160 | B. | y=-10x2+200x-360 | ||
| C. | y=x2-20x+36 | D. | y=-10x2+310x-2340 |
20.一个角的余角是30度,则这个角的补角是( )
| A. | 45度 | B. | 60度 | C. | 90度 | D. | 120度 |