题目内容
5. 如图,在平行四边形纸片ABCD中,AB=a,将纸片沿对角线BD对折,BC边与AD边交于点F,此时AF=BF=AB.
如图,在平行四边形纸片ABCD中,AB=a,将纸片沿对角线BD对折,BC边与AD边交于点F,此时AF=BF=AB.求:(1)BC的长;
(2)重叠部分的面积.
分析 (1)根据折叠的性质以及等边三角形的性质,即可得到∠E=∠EFD,进而得出DE=DF=a,即AD=2a,再根据四边形ABCD是平行四边形,即可得到BC=AD=2a;
(2)先过BG⊥AD于G,求得BG=$\sqrt{3}$AG=$\frac{\sqrt{3}}{2}$a,再根据S△BDF=$\frac{1}{2}$DF×BG进行计算即可.
解答 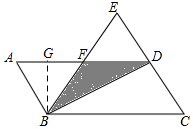 解:(1)由折叠可得,DE=DC=AB=a,∠C=∠E=∠A,
解:(1)由折叠可得,DE=DC=AB=a,∠C=∠E=∠A,
∵AF=BF=AB,
∴△ABF是等边三角形,
∴∠A=∠AFB=∠DFE,AF=AB=a,
∴∠E=∠EFD,
∴DE=DF=a,
∴AD=2a,
∵四边形ABCD是平行四边形,
∴BC=AD=2a;
(2)过BG⊥AD于G,则∠ABG=30°,
∴AG=$\frac{1}{2}$AB=$\frac{1}{2}$a,
∴BG=$\sqrt{3}$AG=$\frac{\sqrt{3}}{2}$a,
∴S△BDF=$\frac{1}{2}$DF×BG=$\frac{1}{2}$a×$\frac{\sqrt{3}}{2}$a=$\frac{\sqrt{3}}{4}$a2,
即重叠部分的面积为$\frac{\sqrt{3}}{4}$a2.
点评 本题主要考查了折叠问题,等边三角形的性质以及平行四边形的性质的运用,解题时注意:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.

练习册系列答案
相关题目
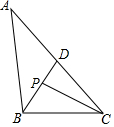 如图,在△ABC中,∠ABC=100°,∠ACB=40°,∠ABC的平分线BD交AC于点D,∠ACB的平分线CP交BD于点D.
如图,在△ABC中,∠ABC=100°,∠ACB=40°,∠ABC的平分线BD交AC于点D,∠ACB的平分线CP交BD于点D.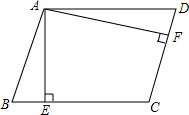 如图,平行四边形ABCD的邻边AD:AB=5:4,过点A作AE⊥BC,AF⊥CD,垂足分别为点E、F,AE=2cm,则AF=2.5cm.
如图,平行四边形ABCD的邻边AD:AB=5:4,过点A作AE⊥BC,AF⊥CD,垂足分别为点E、F,AE=2cm,则AF=2.5cm.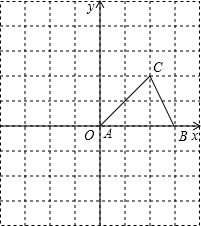 如图,△ABC的顶点A在原点,B、C坐标分别为B(3,0)、C(2,2),将△ABC向左平移2个单位后再向下平移1单位,可得到△A′B′C′.
如图,△ABC的顶点A在原点,B、C坐标分别为B(3,0)、C(2,2),将△ABC向左平移2个单位后再向下平移1单位,可得到△A′B′C′.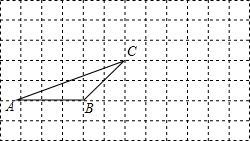 如图,在正方形网格中有一个格点三角形ABC,(即△ABC的各顶点都在格点上),按要求进行下列作图:
如图,在正方形网格中有一个格点三角形ABC,(即△ABC的各顶点都在格点上),按要求进行下列作图: