Question

16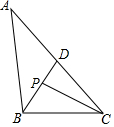．如图，在△ABC中，∠ABC=100°，∠ACB=40°，∠ABC的平分线BD交AC于点D，∠ACB的平分线CP交BD于点D．
（1）BD与AC的位置关系是互相垂直．
（2）求∠BPC的度数．

Answer 1

分析 （1）由∠ABC=100°、BD平分∠ABC，可得出∠DBC=50°，结合∠ACB=40°利用三角形的内角和即可求出∠BDC=90°，继而得出BD与AC的位置关系；
（2）由PC平分∠ACB、∠ACB=40°，可得出∠BCP=20°，结合（1）中的∠DBC=50°利用三角形内角和定理即可求出∠BPC的度数．

解答 解：（1）∵∠ABC=100°，BD平分∠ABC，
∴∠DBC=$\frac{1}{2}$∠ABC=50°，
∴∠BDC=180°-∠DBC-∠BCD=90°，
∴BD⊥AC．
故答案为：互相垂直．
（2）∵PC平分∠ACB，∠ACB=40°，
∴∠BCP=$\frac{1}{2}$∠ACB=20°，
∴∠BPC=180°-∠PBC-∠BCP=180°-50°-20°=110°．

点评 本题考查了三角形内角和定理、角平分线以及垂线，解题的关键是：（1）利用三角形内角和定理求出∠BDC=90°；（2）利用三角形内角和定理求出∠BPC的度数．