题目内容
1.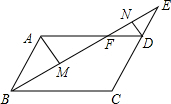 如图,在平行四边形ABCD中,E是CD的延长线上一点,BE与AD交于点F,CD=2DE.M,N分别是BF、EF的中点,若△DEF的面积为a,则AM:DN=2,则?ABCD的面积为12a.
如图,在平行四边形ABCD中,E是CD的延长线上一点,BE与AD交于点F,CD=2DE.M,N分别是BF、EF的中点,若△DEF的面积为a,则AM:DN=2,则?ABCD的面积为12a.
分析 由四边形ABCD是平行四边形,根据平行四边形对边平行且相等,即可得AB∥CD,AD∥BC,AB=CD,然后由平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似,即可判定△DEF∽△CEB,△DEF∽△ABF,又由相似三角形面积的比等于相似比的平方,即可求得答案.
解答 解:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,AB=CD,
∴△DEF∽△CEB,△DEF∽△ABF,
∴$\frac{AB}{DE}=\frac{BF}{EF}$,$\frac{{S}_{△DEF}}{{S}_{△CEB}}$=($\frac{DE}{CE}$)2,$\frac{{S}_{△DEF}}{{S}_{△ABF}}$=($\frac{DE}{AB}$)2,
∵CD=2DE,
∴DE:CE=1:3,DE:AB=1:2,
∴AM:DN=BF:EF=AB:DE=2,
∵S△DEF=a,
∴S△CBE=9a,S△ABF=4a,
∴S四边形BCDF=S△CEB-S△DEF=8a,
∴S?ABCD=S四边形BCDF+S△ABF=8a+4a=12a.
故答案为:2,12a.
点评 此题考查了相似三角形的判定与性质与平行四边形的性质.此题难度适中,注意数形结合思想的应用,注意相似三角形面积的比等于相似比的平方定理的应用.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
11.下列四个结论,其中错误的结论个数为( )
①平行四边形既是轴对称图形,又是中心对称图形;
②平分弦的直径垂直于弦,并且平分弦所对的两条弧;
③经过弦的中点的直径一定垂直于弦;
④相等的圆周角所对的弧相等.
①平行四边形既是轴对称图形,又是中心对称图形;
②平分弦的直径垂直于弦,并且平分弦所对的两条弧;
③经过弦的中点的直径一定垂直于弦;
④相等的圆周角所对的弧相等.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
6.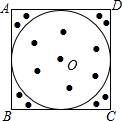 正方形ABCD内,有一个内切圆⊙O.电脑可设计程序:在正方形内可随机产生一系列点,当点数很多时,电脑自动统计正方形内的点数a个,⊙O内的点数b个(在正方形边上和圆上的点不在统计中),根据用频率估计概率的原理,可推得π的大小是( )
正方形ABCD内,有一个内切圆⊙O.电脑可设计程序:在正方形内可随机产生一系列点,当点数很多时,电脑自动统计正方形内的点数a个,⊙O内的点数b个(在正方形边上和圆上的点不在统计中),根据用频率估计概率的原理,可推得π的大小是( )
 正方形ABCD内,有一个内切圆⊙O.电脑可设计程序:在正方形内可随机产生一系列点,当点数很多时,电脑自动统计正方形内的点数a个,⊙O内的点数b个(在正方形边上和圆上的点不在统计中),根据用频率估计概率的原理,可推得π的大小是( )
正方形ABCD内,有一个内切圆⊙O.电脑可设计程序:在正方形内可随机产生一系列点,当点数很多时,电脑自动统计正方形内的点数a个,⊙O内的点数b个(在正方形边上和圆上的点不在统计中),根据用频率估计概率的原理,可推得π的大小是( )| A. | π≈$\frac{a}{b}$ | B. | π≈$\frac{4b}{a}$ | C. | π≈$\frac{b}{a}$ | D. | π≈$\frac{4a}{b}$ |
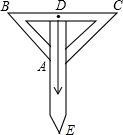 如图是一个三角形测平架,已知AB=AC,在BC的中点D挂一个重锤DE,让其自然下垂,调整架身,使点A恰好在重锤线上,这时AD和BC的位置关系为垂直.
如图是一个三角形测平架,已知AB=AC,在BC的中点D挂一个重锤DE,让其自然下垂,调整架身,使点A恰好在重锤线上,这时AD和BC的位置关系为垂直.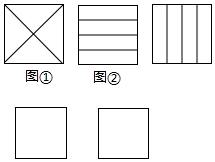 一块正方形空地按下列要求分成四块:(1)被画分割线后整个图形仍是轴对称图形;(2)四个图形形状相同;(3)四个图形面积相等.
一块正方形空地按下列要求分成四块:(1)被画分割线后整个图形仍是轴对称图形;(2)四个图形形状相同;(3)四个图形面积相等.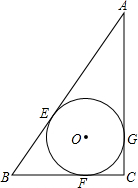 如图所示,在Rt△ABC中,∠C=90°,BC=3,AC=4,⊙O与边AB,BC,AC分别相切于点E,F,G.求⊙O的半径.
如图所示,在Rt△ABC中,∠C=90°,BC=3,AC=4,⊙O与边AB,BC,AC分别相切于点E,F,G.求⊙O的半径.