题目内容
13.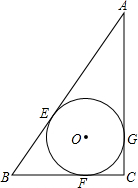 如图所示,在Rt△ABC中,∠C=90°,BC=3,AC=4,⊙O与边AB,BC,AC分别相切于点E,F,G.求⊙O的半径.
如图所示,在Rt△ABC中,∠C=90°,BC=3,AC=4,⊙O与边AB,BC,AC分别相切于点E,F,G.求⊙O的半径.
分析 如图连结OE,OF,OG.先由勾股定理求得AB=5,由⊙O是△ABC的内切圆,∠C=90°,得到四边形CEOF是正方形,根据切线长定理列方程求解即可.
解答 解:如图连结OE,OF,OG.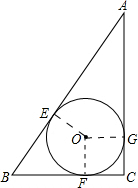
在Rt△ABC中,由勾股定理得:AB=$\sqrt{B{C}^{2}+A{C}^{2}}$=5.
∵⊙O是△ABC的内切圆,
∴∠OGC=∠OFC=90°.
又∵∠C=90°,
∴∠OGC=∠OFC=∠C=90°.
∴四边形ODCF是矩形.
又∵OG=OF,
∴四边形CEOF是正方形.
∴CG=CF=r.
由切线长定理可知:AG=EA,BF=BE.
∴BF+AG=AE+BE=5.
∵BF+r+r+AG=7,
∴5+2r=7.
解得;r=1.
点评 本题主要考查的是三角形的内心、切线的性质、正方形的判定、切线长定义,证得四边形CEOF是正方形是解题的关键.

练习册系列答案
相关题目
3. 如图,利用一面墙,用80米长的篱笆围成一个矩形场地,墙长为30m,围成鸡场的最大面积为( )平方米.
如图,利用一面墙,用80米长的篱笆围成一个矩形场地,墙长为30m,围成鸡场的最大面积为( )平方米.
 如图,利用一面墙,用80米长的篱笆围成一个矩形场地,墙长为30m,围成鸡场的最大面积为( )平方米.
如图,利用一面墙,用80米长的篱笆围成一个矩形场地,墙长为30m,围成鸡场的最大面积为( )平方米.| A. | 800 | B. | 750 | C. | 600 | D. | 2400 |
18.用下列哪种方法解方程3(x-2)2=2x-4比较简便( )
| A. | 直接开平方法 | B. | 配方法 | C. | 公式法 | D. | 因式分解法 |
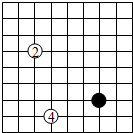 如图,围棋棋盘放置在某个平面直角坐标系内,白棋②的坐标为(-7,-4),白棋④的坐标为(-6,-8),那么黑棋的坐标应该是(-3,-7).
如图,围棋棋盘放置在某个平面直角坐标系内,白棋②的坐标为(-7,-4),白棋④的坐标为(-6,-8),那么黑棋的坐标应该是(-3,-7).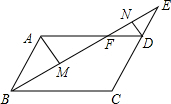 如图,在平行四边形ABCD中,E是CD的延长线上一点,BE与AD交于点F,CD=2DE.M,N分别是BF、EF的中点,若△DEF的面积为a,则AM:DN=2,则?ABCD的面积为12a.
如图,在平行四边形ABCD中,E是CD的延长线上一点,BE与AD交于点F,CD=2DE.M,N分别是BF、EF的中点,若△DEF的面积为a,则AM:DN=2,则?ABCD的面积为12a.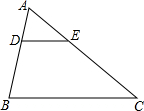 如图,在△ABC中,DE∥BC,AD=2,DB=4,DE=3,则BC的长为9.
如图,在△ABC中,DE∥BC,AD=2,DB=4,DE=3,则BC的长为9.



