题目内容
17.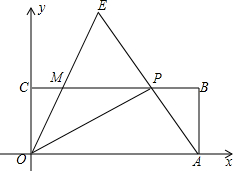 如图,在直角坐标系xOy中,矩形OABC的顶点A、C分别在x轴和y轴正半轴上,点B的坐标是(5,2),点P是CB边上一动点(不与点C、点B重合),连结OP、AP,过点O作射线OE交AP的延长线于点E,交CB边于点M,且∠AOP=∠COM,令CP=x,MP=y.
如图,在直角坐标系xOy中,矩形OABC的顶点A、C分别在x轴和y轴正半轴上,点B的坐标是(5,2),点P是CB边上一动点(不与点C、点B重合),连结OP、AP,过点O作射线OE交AP的延长线于点E,交CB边于点M,且∠AOP=∠COM,令CP=x,MP=y.(1)当x为何值时,OP⊥AP?
(2)求y与x的函数关系式,并写出x的取值范围;
(3)在点P的运动过程中,是否存在x,使△OCM的面积与△ABP的面积之和等于△EMP的面积?若存在,请求x的值;若不存在,请说明理由.
分析 (1)根据相似三角形的判定定理证明△OPC∽△PAB,根据相似三角形的性质列出比例式,得到一元二次方程,解方程即可;
(2)证明△OCM∽△PCO,根据相似三角形的性质列出比例式即可求解;
(3)过E作ED⊥OA于点D,交MP于点F,根据题意得到△EOA的面积=矩形OABC的面积,求出ED的长,根据相似三角形的性质求出PM,由(2)的解析式计算即可.
解答 解:(1)由题意知,OA=BC=5,AB=OC=2,∠B=∠OCM=90°,BC∥OA,
∵OP⊥AP,
∴∠OPC+∠APB=∠APB+∠PAB=90°,
∴∠OPC=∠PAB,
∴△OPC∽△PAB,
∴$\frac{CP}{AB}=\frac{OC}{PB}$,即$\frac{x}{2}=\frac{2}{5-x}$,
解得x1=4,x2=1(不合题意,舍去).
∴当x=4时,OP⊥AP;
(2)∵BC∥OA,
∴∠CPO=∠AOP,
∵∠AOP=∠COM,
∴∠COM=∠CPO,
∵∠OCM=∠PCO,
∴△OCM∽△PCO,
∴$\frac{CM}{CO}=\frac{CO}{CP}$,即$\frac{x-y}{2}=\frac{2}{x}$,
∴$y=x-\frac{4}{x}$,x的取值范围是2<x<5;
(3)假设存在x符合题意,
过E作ED⊥OA于点D,交MP于点F,则DF=AB=2,
∵△OCM与△ABP面积之和等于△EMP的面积,
∴${S_{△EOA}}={S_{矩OABC}}=2×5=\frac{1}{2}×5ED$,
∴ED=4,EF=2,
∵PM∥OA,
∴△EMP∽△EOA,
∴$\frac{EF}{ED}=\frac{MP}{OA}$,即$\frac{2}{4}=\frac{y}{5}$,
解得$y=\frac{5}{2}$,
∴由(2)$y=x-\frac{4}{x}$得,$x-\frac{4}{x}=\frac{5}{2}$,
解得${x_1}=\frac{{5+\sqrt{89}}}{4},{x_2}=\frac{{5-\sqrt{89}}}{4}$(不合题意舍去),
∴在点P的运动过程中,存在$x=\frac{{5+\sqrt{89}}}{4}$,使△OCM与△ABP面积之和等于△EMP的面积.
点评 本题考查的是矩形的性质、相似三角形的判定和性质以及函数解析式的确定,掌握矩形的性质定理、相似三角形的判定定理和性质定理是解题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | $\frac{\sqrt{3}}{8}$ | B. | $\frac{\sqrt{3}}{4}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | $\frac{\sqrt{2}}{8}$ |
| A. | 3x2-x2=3 | B. | a•a3=a3 | C. | a6÷a3=a2 | D. | (a2)3=a6 |
 如图,在Rt△ABC中,∠C=90°,BC=6,AB=10,则tanA=$\frac{3}{4}$.
如图,在Rt△ABC中,∠C=90°,BC=6,AB=10,则tanA=$\frac{3}{4}$.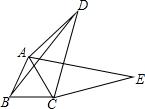 如图,四边形ABCD中,AC,BD是对角线,△ABC是等边三角形.线段CD绕点C顺时针旋转60°得到线段CE,连接AE.
如图,四边形ABCD中,AC,BD是对角线,△ABC是等边三角形.线段CD绕点C顺时针旋转60°得到线段CE,连接AE.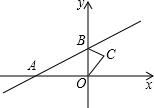 如图,直线y=$\frac{1}{2}$x+1与x轴交于点A,与y轴交于点B,△BOC与△B′O′C′是以点A为位似中心的位似图形,且相似比为1:3,则点B的对应点B′的坐标为(-8,-3)或(4,3).
如图,直线y=$\frac{1}{2}$x+1与x轴交于点A,与y轴交于点B,△BOC与△B′O′C′是以点A为位似中心的位似图形,且相似比为1:3,则点B的对应点B′的坐标为(-8,-3)或(4,3).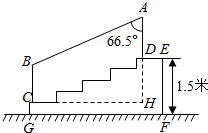 如图,某城市市民广场一入口处有五级高度相等的小台阶.已知台阶总高1.5米,为了安全,现要做一个不锈钢扶手AB及两根与FG垂直且长为1米的不锈钢架杆AD和BC(杆子的底端分别为D、C),且∠DAB=66.5°.(参考数据:cos66.5°≈0.40,sin66.5°≈0.92)
如图,某城市市民广场一入口处有五级高度相等的小台阶.已知台阶总高1.5米,为了安全,现要做一个不锈钢扶手AB及两根与FG垂直且长为1米的不锈钢架杆AD和BC(杆子的底端分别为D、C),且∠DAB=66.5°.(参考数据:cos66.5°≈0.40,sin66.5°≈0.92) 如图,转盘中6个小扇形的面积都相等,任意转动转盘1次,当转盘停止转动时,指针指向红色区域的概率为$\frac{1}{3}$.
如图,转盘中6个小扇形的面积都相等,任意转动转盘1次,当转盘停止转动时,指针指向红色区域的概率为$\frac{1}{3}$.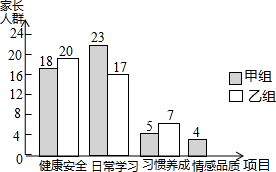 为了了解家长关注孩子成长方面的状况,学校开展了针对学生家长的“您最关心孩子哪方面成长”的主题调查,调查设置了“健康安全”、“日常学习”、“习惯养成”、“情感品质”四个项目,并随机抽取甲、乙两班共100位学生家长进行调查,根据调查结果,绘制了如图不完整的条形统计图.
为了了解家长关注孩子成长方面的状况,学校开展了针对学生家长的“您最关心孩子哪方面成长”的主题调查,调查设置了“健康安全”、“日常学习”、“习惯养成”、“情感品质”四个项目,并随机抽取甲、乙两班共100位学生家长进行调查,根据调查结果,绘制了如图不完整的条形统计图.