题目内容
19.如图1,在正方形ABCD中,点E、F分别为边BC、CD的点,AF、DE相交于点G.如图1,若点E、F不是正方形ABCD的边BC、CD的中点,但满足CE=DF.
(1)如图1线段AF与DE有怎样的数量关系和位置关系?(直接写出结论,不必证明)
(2)如图2,在(1)的基础上,连接AE和EF,若点M、N、P、Q分别为AE、EF、FD、AD的中点,先判断四边形MNPQ是“矩形、菱形、正方形、”中的哪一种,并写出证明过程.
分析 (1)由已知得四边形ABCD为正方形,证明Rt△ADF≌Rt△ECD,然后推出∠ADE+∠DAF=90°;进而得出AF⊥DE;
(2)首先根据题意证明四边形MNPQ是菱形,然后又因为AF⊥DE,得出四边形MNPQ为正方形.
解答 解:(1)AF=DE,且AF⊥DE.理由如下:
∵四边形ABCD为正方形,
∴AD=DC=CB且∠ADC=∠DCB=90°,
在Rt△ADF和Rt△ECD中
$\left\{\begin{array}{l}{AD=DC}\\{∠ADC=∠DCB}\\{CE=DF}\end{array}\right.$,
∴Rt△ADF≌Rt△ECD(SAS),
∴AF=DE,
∴∠DAF=∠CDE,
∵∠ADE+∠CDE=90°,
∴∠ADE+∠DAF=90°,
∴∠AGD=90°,
∴AF⊥DE;
(2)结论:四边形MNPQ是正方形.
证明:∵AM=ME,AQ=QD,
∴MQ∥DE且MQ=$\frac{1}{2}$DE,
同理可证:PN∥DE,PN=$\frac{1}{2}$DE;MN∥AF,MN=$\frac{1}{2}$AF;PQ∥AF,PQ=$\frac{1}{2}$AF;
∵AF=DE,
∴MN=NP=PQ=QM,
∴四边形MNPQ是菱形,
又∵AF⊥DE,
∴∠MQP=90°,
∴四边形MNPQ是正方形.
点评 本题考查的是中点四边形,需要掌握全等三角形的判定,正方形的判定以及正方形的性质,难度一般.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
8.若a、b是有理数,且|a|=1,|b|=2,ab<0,则a+b=( )
| A. | 1或-3 | B. | 3或-1 | C. | 3或-3 | D. | 1或-1 |
12.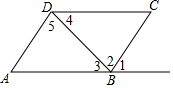 如图,由AD∥BC可以得到的结论是( )
如图,由AD∥BC可以得到的结论是( )
 如图,由AD∥BC可以得到的结论是( )
如图,由AD∥BC可以得到的结论是( )| A. | ∠1=∠2 | B. | ∠1=∠4 | C. | ∠2=∠5 | D. | ∠3=∠4 |
 如图,在平面直角坐标系中,直线l1:y=-$\frac{1}{2}$x+6分别与x轴、y轴交于点B、C,且与直线l2:y=$\frac{1}{2}$x交于点A.
如图,在平面直角坐标系中,直线l1:y=-$\frac{1}{2}$x+6分别与x轴、y轴交于点B、C,且与直线l2:y=$\frac{1}{2}$x交于点A.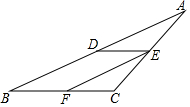 如图,已知DE∥BC,EF平分∠CED,∠A=∠CFE,那么EF与AB平行吗?为什么?
如图,已知DE∥BC,EF平分∠CED,∠A=∠CFE,那么EF与AB平行吗?为什么?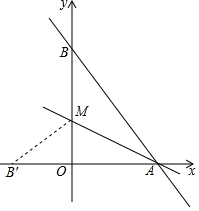 直线y=-$\frac{4}{3}$x+8与x轴、y轴分别交于点A和点B,M是OB上的一点,若将△ABM沿AM折叠,点B恰好落在x轴上的点B′处,则M的坐标为(0,3).
直线y=-$\frac{4}{3}$x+8与x轴、y轴分别交于点A和点B,M是OB上的一点,若将△ABM沿AM折叠,点B恰好落在x轴上的点B′处,则M的坐标为(0,3).