题目内容
9. 如图,在平面直角坐标系中,直线l1:y=-$\frac{1}{2}$x+6分别与x轴、y轴交于点B、C,且与直线l2:y=$\frac{1}{2}$x交于点A.
如图,在平面直角坐标系中,直线l1:y=-$\frac{1}{2}$x+6分别与x轴、y轴交于点B、C,且与直线l2:y=$\frac{1}{2}$x交于点A.(1)求出点A的坐标.
(2)若D是线段OA上的点,且△COD的面积为12,求直线CD的函数表达式.
(3)在(2)的条件下,设P是射线CD上的点,在平面内是否存在点Q,使以O、C、P、Q为顶点的四边形是菱形?若存在,直接写出点P的坐标;若不存在,请说明理由.
分析 (1)联立两直线解析式求出A的坐标即可;
(2)根据D在直线OA上,设出D坐标,表示出三角形COD面积,把已知面积代入求出x的值,确定出D坐标,利用待定系数法求出CD解析式即可;
(3)在(2)的条件下,设P是射线CD上的点,在平面内存在点Q,使以O、C、P、Q为顶点的四边形是菱形,如图所示,分三种情况考虑:(i)当四边形OP1Q1C为菱形时,由∠COP1=90°,得到四边形OP1Q1C为正方形;(ii)当四边形OP2CQ2为菱形时;(iii)当四边形OQ3P3C为菱形时;分别求出P坐标即可.
解答 解:
(1)解方程组$\left\{\begin{array}{l}{y=-\frac{1}{2}x+6}\\{y=\frac{1}{2}x}\end{array}\right.$,得$\left\{\begin{array}{l}{x=6}\\{y=3}\end{array}\right.$,
∴A(6,3);
(2)设D(x,$\frac{1}{2}$x),
∵△COD的面积为12,
∴$\frac{1}{2}$×6×x=12,
解得:x=4,
∴D(4,2),
设直线CD的函数表达式是y=kx+b,
把C(0,6),D(4,2)代入得:$\left\{\begin{array}{l}{6=b}\\{2=4k+b}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-1}\\{b=6}\end{array}\right.$,
∴直线CD解析式为y=-x+6;
(3)在直线l1:y=-$\frac{1}{2}$x+6中,当y=0时,x=12,
∴C(0,6),
存在点P,使以O、C、P、Q为顶点的四边形是菱形,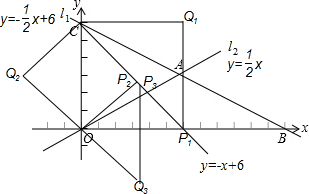
如图所示,分三种情况考虑:
(i)当四边形OP1Q1C为菱形时,由∠COP1=90°,得到四边形OP1Q1C为正方形,此时OP1=OC=6,即P1(6,0);
(ii)当四边形OP2CQ2为菱形时,由C坐标为(0,6),得到P2纵坐标为3,
把y=3代入直线直线CQ的解析式y=-x+6中,可得3=-x+6,解得x=3,此时P2(3,-3);
(iii)当四边形OQ3P3C为菱形时,则有OQ3=OC=CP3=P3Q3=6,设P3(x,-x+6),
∴x2+(-x+6-6)2=62,解得x=3$\sqrt{2}$或x=-3$\sqrt{2}$(舍去),此时P3(3$\sqrt{2}$,-3$\sqrt{2}$+6);
综上可知存在满足条件的点的P,其坐标为(6,0)或(3,-3)或(3$\sqrt{2}$,-3$\sqrt{2}$+6).
点评 本题为一次函数的综合应用,涉及一次函数与坐标轴的交点、待定系数法确定一次函数解析式、一次函数图象的交点、一次函数图象与性质、菱形的性质及分类讨论思想等.在(2)中求得D点坐标是解题的关键,在(3)中确定出P点的位置是解题的关键.本题考查知识点较多,综合性较强,难度适中.

 精英口算卡系列答案
精英口算卡系列答案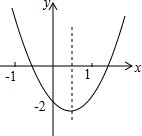 二次函数y=ax2+bx+c的图象如图所示,则下列结论:①abc<0;②b2-4ac>0;③2a+b>0;④a+b+c<0;⑤ax2+bx+c+2=0的解为x=0,其中正确的有( )
二次函数y=ax2+bx+c的图象如图所示,则下列结论:①abc<0;②b2-4ac>0;③2a+b>0;④a+b+c<0;⑤ax2+bx+c+2=0的解为x=0,其中正确的有( )| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
| A. | 3 | B. | 3$\sqrt{3}$ | C. | 6$\sqrt{3}$ | D. | 12 |
 如图,在平面直角坐标系中,点M在第二象限.
如图,在平面直角坐标系中,点M在第二象限.