题目内容
13.已知f(x)=$\frac{1-{x}^{2}}{1+{x}^{2}}$,当x分别取值$\frac{1}{2016}$,$\frac{1}{2015}$,…,$\frac{1}{2}$,1,2,…,2015,求.f($\frac{1}{2016}$)+f($\frac{1}{2015}$)+…+f($\frac{1}{2}$)+F(1)+f(2)…+f(2015)+f(2016).分析 分别求出f(2)+f($\frac{1}{2}$)、f(3)+f($\frac{1}{3}$)、f(4)+f($\frac{1}{4}$)的值,根据值的变化找出规律“f(n)+f($\frac{1}{n}$)=0(n为正整数,且n>1)”,依据该规律即可解决问题.
解答 解:观察,发现规律:f(2)+f($\frac{1}{2}$)=$\frac{1-{2}^{2}}{1+{2}^{2}}$+$\frac{1-(\frac{1}{2})^{2}}{1+(\frac{1}{2})^{2}}$=-$\frac{3}{5}$+$\frac{3}{5}$=0,f(3)+f($\frac{1}{3}$)=$\frac{1-{3}^{2}}{1+{3}^{2}}$+$\frac{1-(\frac{1}{3})^{2}}{1+(\frac{1}{3})^{2}}$=-$\frac{4}{5}$+$\frac{4}{5}$=0,f(4)+f($\frac{1}{4}$)=$\frac{1-{4}^{2}}{1+{4}^{2}}$+$\frac{1-(\frac{1}{4})^{2}}{1+(\frac{1}{4})^{2}}$=-$\frac{15}{17}$+$\frac{15}{17}$=0,…,
∴f(n)+f($\frac{1}{n}$)=0(n为正整数,且n>1).
∴f($\frac{1}{2016}$)+f($\frac{1}{2015}$)+…+f($\frac{1}{2}$)+F(1)+f(2)…+f(2015)+f(2016),
=f($\frac{1}{2016}$)+f(2016)+f($\frac{1}{2015}$)+f(2015)+…+f($\frac{1}{2}$)+f(2)+f(1),
=0.
点评 本题属于规律型中的数字的变化类,解题的关键是找出规律“f(n)+f($\frac{1}{n}$)=0(n为正整数,且n>1)”.本题属于基础题,难度不大,解决该题型题目时,列出部分f(x)+f($\frac{1}{x}$)的值,根据值的变化找出规律是关键.

 名校课堂系列答案
名校课堂系列答案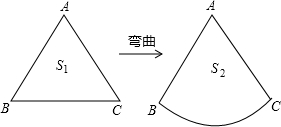 如图,△ABC为等边三角形,保持各边的长度不变,将BC边向三角形外弯曲得到扇形ABC,设△ABC的面积为S1,扇形ABC的面积为S2,则S1与S2的大小关系为( )
如图,△ABC为等边三角形,保持各边的长度不变,将BC边向三角形外弯曲得到扇形ABC,设△ABC的面积为S1,扇形ABC的面积为S2,则S1与S2的大小关系为( )| A. | S1<S2 | B. | S1=S2 | C. | S1>S2 | D. | 无法确定 |